题目内容
10．
如图，已知圆上两点A、B．（1）用直尺和圆规作以AB为底边的圆内接等腰三角形（不写画法，保留痕迹）；
（2）若已知圆的半径R=5，AB=8，求所作等腰三角形底边上的高．
分析 （1）作AB的垂直平分线与圆相交于一点，分别与A、B连接即可得到以AB为底边的圆内接等腰三角形；
（2）连结OA，先根据垂径定理得到AD的长，再根据勾股定理，以及线段的和差关系即可求解．
解答 解：（1）如图所示：△ABC即为所求．
（2）连结OA，
∵圆的半径R=5，AB=8，
∴OA=OC=5，AD=4，
在△AOD中，OD=$\sqrt{{5}^{2}-{4}^{2}}$=3，
∴CD=OC+OD=5+3=8．
故所作等腰三角形底边上的高是8．
点评 本题考查了复杂作图，主要利用了线段垂直平分线的作法，等腰三角形的性质，以及垂径定理．
练习册系列答案
相关题目
如图，D为△ABC的BC边上的任意一点，E为AD的中点，△BEC的面积为5，则△ABC的面积为10．
尺规作图（保留作图痕迹，不写作法）
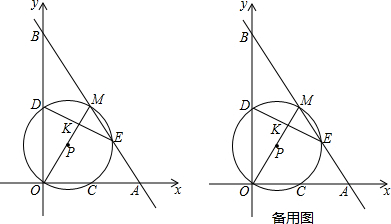
如图，⊙O的半径为5，点P在⊙O外，PB交⊙O于A、B两点，PC交⊙O于D、C两点．