题目内容
如图,边长都是1的正方形和正三角形,其一边在同一水平线上,三角形沿该水平线自左向右匀速穿过正方形.设穿过的时间为t,正方形与三角形重合部分的面积为S(空白部分),那么S关于t的函数大致图象应为( )
A.

B.

C.

D.

【答案】分析:根据边长都是1的正方形和正三角形,可知三角形进入正方形当0≤t≤ 时,以及当
时,以及当 <t<1时,当1<t≤
<t<1时,当1<t≤ 时以及当
时以及当 <t≤2时,求出函数关系式,即可得出答案.
<t≤2时,求出函数关系式,即可得出答案.
解答:解:∵边长都是1的正方形和正三角形,其一边在同一水平线上,三角形沿该水平线自左向右匀速穿过正方形.
穿过的时间为t,正方形与三角形重合部分的面积为S(空白部分),
∴S关于t的函数大致图象应为:三角形进入正方形以前是空白面积逐渐增大,当0≤t≤ 时,S=
时,S= ×t×
×t× t=
t= t2,
t2,
当 <t≤1时,S=
<t≤1时,S= ×1×
×1× -
- ×(1-t)×
×(1-t)× (1-t)=-
(1-t)=- t2+
t2+ t-
t- ,
,
当1<t≤ 时,S=
时,S= ×1×
×1× -
- ×(t-1)×
×(t-1)× (t-1)=-
(t-1)=- t2+
t2+ t-
t- ,
,
当 <t≤2时,S=
<t≤2时,S= ×(2-t)×
×(2-t)× (2-t)=
(2-t)= t2-2
t2-2 t+2
t+2 ,
,
∴S与t是二次函数关系.
∴只有D符合要求.
故选D.
点评:此题主要考查了函数图象中动点问题,根据移动路线以及图形边长即可得出空白面积的函数关系式情况是解决问题的关键.
 时,以及当
时,以及当 <t<1时,当1<t≤
<t<1时,当1<t≤ 时以及当
时以及当 <t≤2时,求出函数关系式,即可得出答案.
<t≤2时,求出函数关系式,即可得出答案.解答:解:∵边长都是1的正方形和正三角形,其一边在同一水平线上,三角形沿该水平线自左向右匀速穿过正方形.
穿过的时间为t,正方形与三角形重合部分的面积为S(空白部分),
∴S关于t的函数大致图象应为:三角形进入正方形以前是空白面积逐渐增大,当0≤t≤
 时,S=
时,S= ×t×
×t× t=
t= t2,
t2,当
 <t≤1时,S=
<t≤1时,S= ×1×
×1× -
- ×(1-t)×
×(1-t)× (1-t)=-
(1-t)=- t2+
t2+ t-
t- ,
,当1<t≤
 时,S=
时,S= ×1×
×1× -
- ×(t-1)×
×(t-1)× (t-1)=-
(t-1)=- t2+
t2+ t-
t- ,
,当
 <t≤2时,S=
<t≤2时,S= ×(2-t)×
×(2-t)× (2-t)=
(2-t)= t2-2
t2-2 t+2
t+2 ,
,∴S与t是二次函数关系.
∴只有D符合要求.
故选D.
点评:此题主要考查了函数图象中动点问题,根据移动路线以及图形边长即可得出空白面积的函数关系式情况是解决问题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
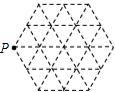 如图,在由24个边长都为1的小正三角形的网格中,点P是正六边形的一个顶点,Q在网格中的格点(即小正三角形的顶点)上,若以点P,Q为端点的线段的长为无理数,请你写出所有可能的线段PQ的长
如图,在由24个边长都为1的小正三角形的网格中,点P是正六边形的一个顶点,Q在网格中的格点(即小正三角形的顶点)上,若以点P,Q为端点的线段的长为无理数,请你写出所有可能的线段PQ的长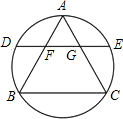 如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )
如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )
 C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.
C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.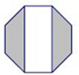 如图是一个正八边形,它的8条边长都是2cm,每个内角都是135°,则图中阴影部分的面积和非阴影部分的面积之差为( )cm2.
如图是一个正八边形,它的8条边长都是2cm,每个内角都是135°,则图中阴影部分的面积和非阴影部分的面积之差为( )cm2.