Question

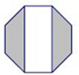如图是一个正八边形，它的8条边长都是2cm，每个内角都是135°，则图中阴影部分的面积和非阴影部分的面积之差为（　　）cm²．

• A、2

  2

• B、2
• C、1
• D、0

Answer 1

分析：根据题意可得两阴影部分分别为等腰梯形，根据内角为135°，边长为2，可分别求出HO、AF的长，然后可求出阴影部分及飞阴影部分的面积，从而可得出两者之差．

解答：解：过点H作HO⊥AF于点O，过点G作GM⊥AF于点M，
由题意得，∠HAO=45°，AH=2，∠GFM=45°，GF=2，
在RT△AHO中可得，HO=AHsin∠HAO=

2

，AO=AHcos∠HAO=

2

，
在RT△GMF中可得，GM=AHsin45°=

2

，MF=GFcos45°=

2

，
∴可得AF=

2

+2+

2

=2+2

2

，
故可得阴影部分的面积=2×

1

2

（HG+AF）×HO=4

2

+4，非阴影部分的面积=AB×AF=4+4

2

，
∴图中阴影部分的面积和非阴影部分的面积之差为0cm²．
故选D．

点评：本题考查了面积及等积变换，结合考查了等腰梯形的知识，利用等腰梯形的性质求出HO，AF的长度是解答本题的关键，难度一般，注意细心运算．