题目内容
小明家为响应节能减排号召，计划利用两年时间，将家庭每年人均碳排放量由目前的3245kg减至2000kg．设小明家每年人均碳排放量的平均减少率为x，则下面列出的方程中正确的是（ ）
| A、3245（1-2x）=2000 |
| B、2000（1+x）2=3245 |
| C、3245（1-x）2=2000 |
| D、2000（1+2x）=3245 |
考点：由实际问题抽象出一元二次方程
专题：增长率问题
分析：降低后的排放量=降低前的排放量×（1-降低率），如果设小明家每年人均碳排放量的平均减少率为x，则第一次降低后的排放量是3245（1-x），那么第二次降低后的排放量是3245（1-x）2，即可列出方程．
解答：解：设小明家每年人均碳排放量的平均减少率为x，则
3245（1-x）2=2000．
故选C．
3245（1-x）2=2000．
故选C．
点评：本题考查了由实际问题抽象出一元二次方程．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，从而列出方程．
练习册系列答案
考前必练系列答案
相关题目
用代数式表示“两数的和的平方”是（ ）
| A、（a+b）2 |
| B、a2+b2 |
| C、a2+b |
| D、a+b2 |
二次函数y=-
（x+2）2-6的对称轴是（ ）
| 1 |
| 3 |
| A、直线x=-6 | ||
| B、直线x=2 | ||
C、直线x=-
| ||
| D、直线x=-2 |
抛物线y=x2-6x+5的对称轴为（ ）
| A、x=3 | ||
| B、x=-3 | ||
| C、x=6 | ||
D、x=-
|
已知：2a=-a，则数a等于（ ）
| A、不确定 | B、1 | C、-1 | D、0 |
二次函数y=2（x-3）2-1的图象的对称轴是（ ）
| A、直线x=-3 |
| B、直线x=3 |
| C、直线x=-1 |
| D、直线x=1 |
某市2012年的地方公共财政收入，用四舍五入法取近似值后为27.19亿元，那么这个数值（ ）
| A、精确到亿位 |
| B、精确到百分位 |
| C、精确到千万位 |
| D、精确到百万位 |
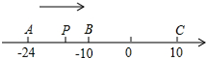已知数轴上有A、B、C三个点，分别表示有理数-24，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．