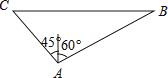Question

【题目】如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（ ）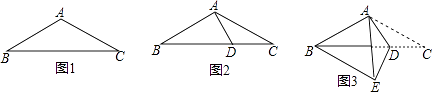

A.4
B.
C.3
D.2

Answer 1

【答案】B
【解析】解：∵AB=AC，
∴∠ABC=∠C，
∵∠DAC=∠ACD，
∴∠DAC=∠ABC，
∵∠C=∠C，
∴△CAD∽△CBA，
∴ ，
∴ = ，
∴CD= ，BD=BC﹣CD= ，
∵∠DAM=∠DAC=∠DBA，∠ADM=∠ADB，
∴△ADM∽△BDA，
∴ = ，即 = ，
∴DM= ，MB=BD﹣DM= ，
∵∠ABM=∠C=∠MED，
∴A、B、E、D四点共圆，
∴∠ADB=∠BEM，∠EBM=∠EAD=∠ABD，
∴△ABD∽△MBE，
∴ = ，
∴BE= = = ．
故选B．

只要证明△ABD∽△MBE，得 = ，只要求出BM、BD即可解决问题．本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是充分利用相似三角形的性质解决问题，本题需要三次相似解决问题，题目比较难，属于中考选择题中的压轴题．