题目内容
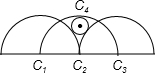
如图，半圆O的直径AB=4，⊙O1与半圆O外切，并且与射线BA切于点M，若AM=3，则⊙O1的半径是______．
AO2=2，
设⊙O1的半径是r，
连接O1M，O1O2，
∵⊙O1与半圆O外切，并且与射线BA切于点M，
∴O1O2=2+r，O1M=r，O1M⊥AB，
MO2=5
由勾股定理得：O1O22=O1M2+MO22，
即（2+r）2=r2+52，
解得：r=
，
故答案为：
．
设⊙O1的半径是r，
连接O1M，O1O2，
∵⊙O1与半圆O外切，并且与射线BA切于点M，
∴O1O2=2+r，O1M=r，O1M⊥AB，
MO2=5
由勾股定理得：O1O22=O1M2+MO22，
即（2+r）2=r2+52，
解得：r=
| 21 |
| 4 |
故答案为：
| 21 |
| 4 |
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
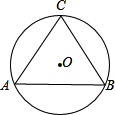
在剩余铁片上截下一个充分大的圆铁片⊙O2，如图．
