Question

【题目】已知：如图，Rt△ABC中，∠BAC＝90°，AB＝AC，D是BC的中点，AE＝BF．若BC＝8，则四边形AFDE的面积是_____．

Answer 1

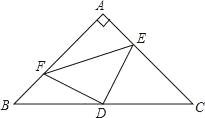
【答案】8．

【解析】

连接AD，证明△BFD≌△AED，根据全等三角形的性质即可得出，得到四边形AFDE的面积=S△ABD=S△ABC，于是得到结论．

连接AD,

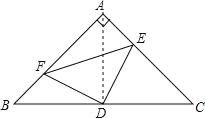
∵Rt△ABC中,∠BAC=90，AB=AC，

∴∠B=∠C=45，

∵AB=AC，DB=CD，

∴∠DAE=∠BAD=45，

∴∠BAD=∠B=45，

∴AD=BD,∠ADB=90，

在△DAE和△DBF中，

，

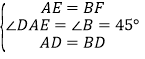∴△DAE≌△DBF(SAS)，

∴，

∴四边形AFDE的面积=S△ABD=S△ABC，

∵BC=8，

∴AD=BC=4，

∴四边形AFDE的面积=S△ABD=S△ABC=××8×4=8.

故答案为：8.