题目内容
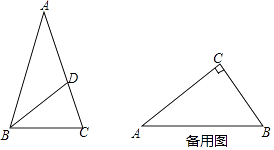
【题目】如何求tan75°的值？按下列方法作图可解决问题.如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BM上截取线段BD，使BD=AB，连接AD.连接此图可求得tan75°的值为（ ）
A.2- 
B.2+
C.1+
D.
-1
【答案】B
【解析】解：在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，
则AB=2AC=2k，BC= 
AC= k.
∵BD=AB=2k，
∴CD=BC+BD=（ +2）k，∠BDA= 
∠ABC=15°，
∴∠CAD=75°，
则在Rt△ACD中，tan75°=tan∠CAD= 
.
故选B.
解直角三角形，求正切值时，需要知道直角三角形的两条边，由AC=k，则易得CD的长，而∠CAD=75°，即可解答.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产
、
两种产品共50件．已知生产一件种产品需用甲种原料9千克，乙种原料3千克，可获利润700元；生产一件种产品需用甲种原料4千克，乙种原料10千克，可获利润1200元．
（1）设生产种产品
件，完成表格：
|
| |
生产数量（件 |
| 件 |
需甲种原料（千克） |
|
|
需乙种原料（千克） |
|
|
（2）按要求安排、两种产品的件数有几种方案？请你设计出来．
（3）以上方案哪种利润最大？是多少元？
