Ő‚ńŅńŕ»›
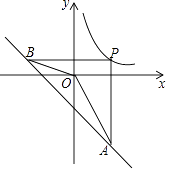
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=ax2+bx+4ĹĽy÷Š”ŕĶ„A£¨≤Ęĺ≠ĻżB£®4£¨4£©ļÕC£®6£¨0£©ŃĹĶ„£¨Ķ„DĶń◊ÝĪÍő™£®4£¨0£©£¨Ń¨Ĺ”AD£¨AB£¨BC£¨Ķ„Eī”Ķ„A≥Ų∑Ę£¨“‘√Ņ√Ž ![]() łŲĶ•őĽ≥§∂»ĶńňŔ∂»—ōŌŖ∂őADŌÚĶ„D‘ň∂Į£¨ĶĹīÔĶ„Dļů£¨“‘√Ņ√Ž1łŲĶ•őĽ≥§∂»ĶńňŔ∂»—ō…šŌŖDC‘ň∂Į£¨…ŤĶ„EĶń‘ň∂Į Īľšő™t√Ž£¨ĻżĶ„E◊ųABĶńīĻŌŖEFĹĽ÷ĪŌŖAB”ŕĶ„F£¨“‘ŌŖ∂őEFő™–ĪĪŖŌÚ”“◊ųĶ»—Ł÷ĪĹ«°ųEFG£ģ
łŲĶ•őĽ≥§∂»ĶńňŔ∂»—ōŌŖ∂őADŌÚĶ„D‘ň∂Į£¨ĶĹīÔĶ„Dļů£¨“‘√Ņ√Ž1łŲĶ•őĽ≥§∂»ĶńňŔ∂»—ō…šŌŖDC‘ň∂Į£¨…ŤĶ„EĶń‘ň∂Į Īľšő™t√Ž£¨ĻżĶ„E◊ųABĶńīĻŌŖEFĹĽ÷ĪŌŖAB”ŕĶ„F£¨“‘ŌŖ∂őEFő™–ĪĪŖŌÚ”“◊ųĶ»—Ł÷ĪĹ«°ųEFG£ģ
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©ĶĪĶ„G¬š‘ŕĶŕ“ĽŌůŌřńŕĶńŇ◊őÔŌŖ…Ō Ī£¨«ů≥ŲtĶń÷Ķ£Ľ
£®3£©…ŤĶ„Eī”Ķ„A≥Ų∑Ę Ī£¨Ķ„E£¨F£¨G∂ľ”ŽĶ„A÷ōļŌ£¨Ķ„E‘ŕ‘ň∂ĮĻż≥Ő÷–£¨ĶĪ°ųBCGĶń√śĽżő™4 Ī£¨÷ĪĹ”–ī≥ŲŌŗ”¶Ķńt÷Ķ£¨≤Ę÷ĪĹ”–ī≥ŲĶ„Gī”≥Ų∑ĘĶĹīň Īňýĺ≠ĻżĶń¬∑ĺ∂≥§£ģ
°ĺīūįł°Ņ
£®1£©Ĺ‚£ļĹęB£®4£¨4£©ļÕC£®6£¨0£©īķ»ŽŇ◊őÔŌŖy=ax2+bx+4Ķ√£ļ
![]() £¨
£¨
Ĺ‚Ķ√£ļ 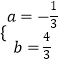 £¨
£¨
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™£ļy=©Ā ![]() x2+
x2+ ![]() x+4
x+4
£®2£©Ĺ‚£ļ»ÁÕľ1£¨”…Ő‚“‚Ķ√£ļAE= ![]() t£¨
t£¨ 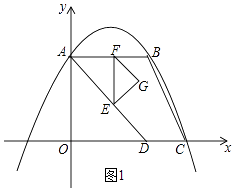
°ŖA£®0£¨4£©£¨B£®4£¨4£©£¨
°ŗAB°Õy÷Š£¨«“AB°őx÷Š£¨
°ŖOA=OD=4£¨
°ŗ°ųAOD «Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨
°ŗ°ŌADO=°ŌBAD=45°„£¨
°ŗ°ųAFE «Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨
°ŗAF=EF=t£¨
°Ŗ°ųEFG «Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨
°ŗG£®t+ ![]() t£¨4©Ā
t£¨4©Ā ![]() t£©£¨
t£©£¨
ľī£ļĶ„G£® ![]() £¨4©Ā
£¨4©Ā ![]() t£©£¨
t£©£¨
ĹęĶ„G£® ![]() £¨4©Ā
£¨4©Ā ![]() t£©īķ»ŽĶĹŇ◊őÔŌŖĶ√£ļ
t£©īķ»ŽĶĹŇ◊őÔŌŖĶ√£ļ
4©Ā ![]() t=©Ā
t=©Ā ![]() £®
£® ![]() £©2+
£©2+ ![]() +4£¨
+4£¨
Ĺ‚Ķ√£ļt1=0£®…Š£©£¨t2= ![]() £¨
£¨
īū£ļĶĪt= ![]() Ī£¨Ķ„G¬š‘ŕŇ◊őÔŌŖ…Ō
Ī£¨Ķ„G¬š‘ŕŇ◊őÔŌŖ…Ō
£®3£©Ĺ‚£ļ»ÁÕľ2£¨Ń¨Ĺ”BD£¨ĶĪG‘ŕBD…Ō Ī£¨
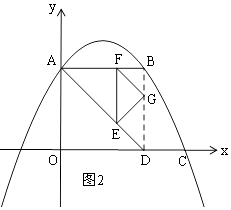
![]() =4£¨
=4£¨
t= ![]() £¨
£¨
ĘŔĶĪ0°‹t°‹ ![]() Ī£¨»ÁÕľ3£¨
Ī£¨»ÁÕľ3£¨ 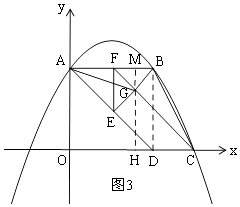
ĻżG◊ųGH°Õx÷Š”ŕH£¨—”≥§HGĹĽAB”ŕM£¨‘ÚGM°ÕAB£¨
°ŖB£®4£¨4£©£¨D£®4£¨0£©£¨
°ŗBD°Õx÷Š£¨
°ŗS°ųBCG=SŐ›–őGHDB+S°ųBDC©ĀS°ųGHC£¨
4= ![]() £®4©Ā
£®4©Ā ![]() +4£©£®4©Ā
+4£©£®4©Ā ![]() £©+
£©+ ![]() °Ń4°Ń£®6©Ā4£©©Ā
°Ń4°Ń£®6©Ā4£©©Ā ![]() £®6©Ā
£®6©Ā ![]() £©£®4©Ā
£©£®4©Ā ![]() t£©£¨
t£©£¨
4= ![]() t£¨
t£¨
Ĺ‚Ķ√£ļt= ![]() £¨
£¨
°ŗAM= ![]() =
= ![]() °Ń
°Ń ![]() =
= ![]() £¨
£¨
GM= ![]() t=
t= ![]() °Ń
°Ń ![]() =
= ![]() £¨
£¨
‘ŕRt°ųAGM÷–£¨”…ĻīĻ…∂®ņŪĶ√£ļAG= ![]() =
= ![]() =
= ![]() £Ľ
£Ľ
°ŗĶĪt= ![]() Ī£¨īň ĪĶ„G‘ň∂ĮĶń¬∑ĺ∂≥§ő™
Ī£¨īň ĪĶ„G‘ň∂ĮĶń¬∑ĺ∂≥§ő™ ![]() £Ľ
£Ľ
ĘŕĶĪG‘ŕBC…Ō Ī£¨»ÁÕľ4£¨ 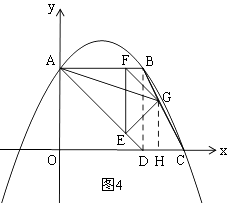
tan°ŌC= ![]() =2£¨
=2£¨
°ŗGH=2HC£¨
°ŗ4©Ā ![]() t=2£®6©Ā
t=2£®6©Ā ![]() £©£¨
£©£¨
t= ![]() £¨
£¨
ĶĪ ![]() £ľt°‹
£ľt°‹ ![]() Ī£¨»ÁÕľ5£¨
Ī£¨»ÁÕľ5£¨ 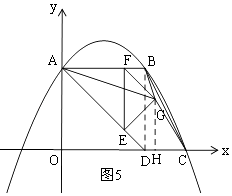
S°ųBCG=S°ųBDC©ĀSŐ›–őBDHG©ĀS°ųGHC£¨
4= ![]() °Ń4°Ń2©Ā
°Ń4°Ń2©Ā ![]() £®4©Ā
£®4©Ā ![]() +4£©£®
+4£©£® ![]() t©Ā4£©©Ā
t©Ā4£©©Ā ![]() °Ń
°Ń ![]() £¨
£¨
t= ![]() £®≤Ľ‘ŕīň∑∂őßńŕ£¨≤Ľ∑ŻļŌŐ‚“‚£©£¨
£®≤Ľ‘ŕīň∑∂őßńŕ£¨≤Ľ∑ŻļŌŐ‚“‚£©£¨
ĘŘĶĪE”ŽD÷ōļŌ Ī£¨F”ŽB÷ōļŌ£¨»ÁÕľ6£¨ 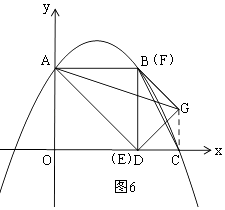
t= ![]() =4£¨
=4£¨
°ŗG£®6£¨2£©£¨
°ŗAG= ![]() =2
=2 ![]() £¨
£¨
°ŗS°ųBCG=SŐ›–őBDCG©ĀS°ųBDC= ![]() °Ń2°Ń£®4+2£©©Ā
°Ń2°Ń£®4+2£©©Ā ![]() °Ń2°Ń4=2£¨
°Ń2°Ń4=2£¨
°ŗĶĪt£ĺ4 Ī£¨»ÁÕľ7£¨ 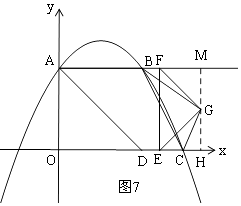
”…Ő‚“‚Ķ√£ļDE=t©Ā4£¨
°ŗOE=t©Ā4+4=t£¨
°ŗOH=OE+EH=t+2£¨
EH=2£¨GM=GH=2£¨
BM=t+2©Ā4=t©Ā2£¨
CH=t+2©Ā6=t©Ā4£¨
ĻżG◊ųMH°Õx÷Š£¨ĹĽx÷Š”ŕH£¨ĹĽ÷ĪŌŖAB”ŕM£¨
°ŗS°ųBGC=SŐ›–őBCHM©ĀS°ųBGM©ĀS°ųGCH£¨
4= ![]() £®t©Ā4+t©Ā2£©°Ń4©Ā
£®t©Ā4+t©Ā2£©°Ń4©Ā ![]() °Ń2°Ń£®t©Ā2£©©Ā
°Ń2°Ń£®t©Ā2£©©Ā ![]() °Ń2°Ń£®t©Ā4£©£¨
°Ń2°Ń£®t©Ā4£©£¨
t=5£¨
ĶĪt=5 Ī£¨Ķ„GĶń‘ň∂Į¬∑ĺ∂∑÷ő™ŃĹ≤Ņ∑÷◊ť≥…£ļ
i£©Ķ„Gī”A‘ň∂ĮĶĹD Ī£¨‘ň∂Į¬∑ĺ∂ő™£ļ»ÁÕľ6÷–ĶńAG≥§£¨ľīő™2 ![]() £Ľ
£Ľ
ii£©Ķ„Gī”DĶ„ľŐ–Ý‘ŕ…šŌŖDC…Ō‘ň∂Į1√Ž Ī£¨¬∑ĺ∂ő™1£Ľ
ňý“‘ĶĪt=5 Ī£¨īň ĪĶ„G‘ň∂ĮĶń¬∑ĺ∂≥§∂»ő™1+2 ![]() £ģ
£ģ
◊Ř…Ōňý Ų£ļĶĪt1= ![]() √Ž£¨īň Ī¬∑ĺ∂≥§∂»ő™
√Ž£¨īň Ī¬∑ĺ∂≥§∂»ő™ ![]() £¨
£¨
ĶĪt2=5√Ž£¨īň Ī¬∑ĺ∂≥§∂»ő™1+2 ![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ£®1£©ņŻ”√īż∂®ŌĶ ż∑®į—B°ĘC◊ÝĪÍīķ»ŽĹ‚őŲ ĹľīŅ…;£®2£©”√t Ķńīķ ż ĹĪŪ ĺ≥ŲGĶńļŠ◊›◊ÝĪÍ£¨īķ»ŽŇ◊őÔŌŖĹ‚őŲ ĹľīŅ…£Ľ£®3£©t=![]() Ī£¨EĶĹD£¨“Úīň Īľšt ∑÷ő™ĶĪĘŔ0°‹t°‹
Ī£¨EĶĹD£¨“Úīň Īľšt ∑÷ő™ĶĪĘŔ0°‹t°‹ ![]() £¨ Ęŕ
£¨ Ęŕ ![]() £ľt
£ľt![]()
![]() ĘŘt=4 4)t£ĺ4;5).t=5 Ī£¨Ķ„GĶń‘ň∂Į¬∑ĺ∂∑÷ő™ŃĹ≤Ņ∑÷◊ť≥…,◊ŘļŌ∆ūņīt=
ĘŘt=4 4)t£ĺ4;5).t=5 Ī£¨Ķ„GĶń‘ň∂Į¬∑ĺ∂∑÷ő™ŃĹ≤Ņ∑÷◊ť≥…,◊ŘļŌ∆ūņīt=![]() ĽÚt=5,∑÷Īū«ů≥Ų∂‘”¶Ķń¬∑ĺ∂≥§.
ĽÚt=5,∑÷Īū«ů≥Ų∂‘”¶Ķń¬∑ĺ∂≥§.

 —ßŃ∑Ņž≥ĶĶņŅžņ÷ľŔ∆ŕ ÓľŔ◊ų“Ķ–¬Ĺģ»ň√Ů≥Ųįś…ÁŌĶŃ–īūįł
—ßŃ∑Ņž≥ĶĶņŅžņ÷ľŔ∆ŕ ÓľŔ◊ų“Ķ–¬Ĺģ»ň√Ů≥Ųįś…ÁŌĶŃ–īūįł ’„īů”Ň—ß–°—ßńÍľ∂ŌőĹ”Ķľ”ŽŃ∑’„Ĺ≠īů—ß≥Ųįś…ÁŌĶŃ–īūįł
’„īů”Ň—ß–°—ßńÍľ∂ŌőĹ”Ķľ”ŽŃ∑’„Ĺ≠īů—ß≥Ųįś…ÁŌĶŃ–īūįł –°—ß ÓľŔ◊ų“Ķ∂ęńŌīů—ß≥Ųįś…ÁŌĶŃ–īūįł
–°—ß ÓľŔ◊ų“Ķ∂ęńŌīů—ß≥Ųįś…ÁŌĶŃ–īūįł ĹÚ«ŇĹŐ”ż ÓľŔįőłŖŌőĹ”Ļ„∂ę»ň√Ů≥Ųįś…ÁŌĶŃ–īūįł
ĹÚ«ŇĹŐ”ż ÓľŔįőłŖŌőĹ”Ļ„∂ę»ň√Ů≥Ųįś…ÁŌĶŃ–īūįł