题目内容
若a为方程x2+x-5=0的解，则a2+a+7的值为（ ）
| A、6 | B、16 | C、9 | D、12 |
考点：一元二次方程的解
专题：
分析：先根据一元二次方程的解的定义得到a2+a-5=0，则a2+a=5，然后利用整体代入的方法计算a2+a+7的值．
解答：解：∵a为方程x2+x-5=0的解，
∴a2+a-5=0，
∴a2+a=5，
∴a2+a+7=5+7=12．
故选：D．
∴a2+a-5=0，
∴a2+a=5，
∴a2+a+7=5+7=12．
故选：D．
点评：本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以一元二次方程的解也称为一元二次方程的根．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
如图，AC⊥BC，DE⊥AC，CD⊥AB，∠1=∠2，试说明GF⊥AB．
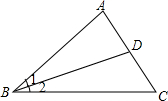如图，下列说法：①∠1就是∠ABC；②∠2就是∠DBC；③以B为顶点的角有3个，他们是∠1，∠2，∠ABC；④∠ADB也可以表示成∠D，⑤∠BCD也可以表示成∠ACB，还可以表示成∠C，其中说法正确的有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
如图所示，该几何体从正面看的形状图是（ ）A、 |
B、 |
C、 |
D、 |