题目内容
8.已知:Rt△ABC中,∠ABC=90°,AB=3,BC=4,以点A,点B为圆心的⊙A,⊙B外切,以点C为圆心的⊙C分别与⊙A,⊙B内切,求⊙A,⊙B,⊙C的半径长.分析 由勾股定理求出斜边AC,设⊙A,⊙B,⊙C的半径长分别为x、y、z;根据题意得出方程组,解方程组即可.
解答  解:如图所示:
解:如图所示:
∵∠ABC=90°,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
设⊙A,⊙B,⊙C的半径长分别为x、y、z;
根据题意得:$\left\{\begin{array}{l}{x+y=3}&{\;}\\{z-y=4}&{\;}\\{z-x=5}&{\;}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}&{\;}\\{y=2}&{\;}\\{z=6}&{\;}\end{array}\right.$.
故⊙A,⊙B,⊙C的半径长分别为1,2,6.
点评 本题考查了勾股定理、相切两圆的性质;熟练掌握相切两圆的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
19.下列各组命题不成立的是( )
| A. | 平行四边形的对边平行且相等 | |
| B. | 依次连结矩形各边中点所得的四边形是菱形 | |
| C. | 三角形的重心是三条中线的交点 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
3.下列表格给出了第28届奥运会上获得金牌前四名的国家的奖牌情况,请制作扇形统计图反映以下四个国家获得奖牌总数的情况.
| 国家 | 金牌 | 银牌 | 铜牌 |
| 美国 | 35 | 39 | 29 |
| 中国 | 32 | 17 | 14 |
| 俄罗斯 | 27 | 27 | 38 |
| 澳大利亚 | 17 | 16 | 16 |
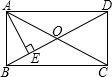 如图,矩形ABCD中,∠DAE:∠BAE=3:1,AE⊥BD,则∠EAC等于45°.
如图,矩形ABCD中,∠DAE:∠BAE=3:1,AE⊥BD,则∠EAC等于45°.