题目内容
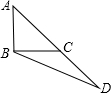 如图,在△ABD中,C为AD上一点,AB=CD=1,∠ABC=90°,∠CBD=30°,则AC=
如图,在△ABD中,C为AD上一点,AB=CD=1,∠ABC=90°,∠CBD=30°,则AC=
- A.1
- B.

- C.

- D.

B
分析:①首先利用有30°角的直角三角形的性质和勾股定理,设BE为x,求得DE用x表示;②作DE垂直于AB的延长线于点E,设AC为y,利用平行线分线段成比例,用x表示y;③再利用△ABC∽△AED,求得BC(用含x的式子表示),最后在Rt△ABC中再利用勾股定理建立方程,求出x,从而解决问题.
解答: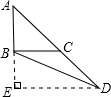 解:如图,作DE垂直于AB的延长线于点E,
解:如图,作DE垂直于AB的延长线于点E,
在Rt△BED中,∠EBD=180°-∠ABC-∠CBD=180°-90°-30°=60°,
∴∠BDE=30°,
∴BD=2BE,设BE为x,则DE=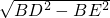 =
= x;
x;
∵∠ABC=90°,∠AED=90°,
∴BC∥ED,
∴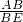 =
= ,设AC为y,则y=
,设AC为y,则y= ;
;
又△ABC∽△AED,
∴ =
= ,
,
即 =
=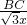 ,则BC=
,则BC= ;
;
在Rt△ABC中,
AB2+BC2=AC2,
即12+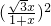 =
=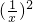 ,
,
整理得4x4+2x3-2x-1=0,
(2x+1)(2x3-1)=0,
∴2x3-1=0,
x=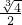 ,
,
∴AC= =
= ;
;
故选B.
点评:此题综合考查了勾股定理,相似三角形的判定与性质以及平行线分线段成比例等知识,属于综合题目.
分析:①首先利用有30°角的直角三角形的性质和勾股定理,设BE为x,求得DE用x表示;②作DE垂直于AB的延长线于点E,设AC为y,利用平行线分线段成比例,用x表示y;③再利用△ABC∽△AED,求得BC(用含x的式子表示),最后在Rt△ABC中再利用勾股定理建立方程,求出x,从而解决问题.
解答:
 解:如图,作DE垂直于AB的延长线于点E,
解:如图,作DE垂直于AB的延长线于点E,在Rt△BED中,∠EBD=180°-∠ABC-∠CBD=180°-90°-30°=60°,
∴∠BDE=30°,
∴BD=2BE,设BE为x,则DE=
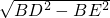 =
= x;
x;∵∠ABC=90°,∠AED=90°,
∴BC∥ED,
∴
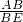 =
= ,设AC为y,则y=
,设AC为y,则y= ;
;又△ABC∽△AED,
∴
 =
= ,
,即
 =
=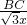 ,则BC=
,则BC= ;
;在Rt△ABC中,
AB2+BC2=AC2,
即12+
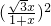 =
=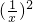 ,
,整理得4x4+2x3-2x-1=0,
(2x+1)(2x3-1)=0,
∴2x3-1=0,
x=
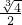 ,
,∴AC=
 =
= ;
;故选B.
点评:此题综合考查了勾股定理,相似三角形的判定与性质以及平行线分线段成比例等知识,属于综合题目.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
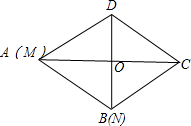 连接BC.
连接BC.
 如图,在△ABD中,∠B=90°,C是BD上一点,DC=10,∠ADB=45°,∠ACB=60°,求AB的长.
如图,在△ABD中,∠B=90°,C是BD上一点,DC=10,∠ADB=45°,∠ACB=60°,求AB的长. (2012•溧水县一模)如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.
(2012•溧水县一模)如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C. 如图,在△ABD中,∠ABC=45゜,AC、BF为高,AC、BF相交于E点.
如图,在△ABD中,∠ABC=45゜,AC、BF为高,AC、BF相交于E点.