Question

如图，在△ABD中，AB=AD，AO平分∠BAD，过点D作AB的平行线交AO的延长线于点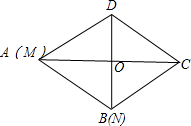C，连接BC．
（1）求证：四边形ABCD是菱形；
（2）如果OA，OB（OA＞OB）的长（单位：米）是一元二次方程x²-7x+12=0的两根，求AB的长以及菱形ABCD的面积；
（3）若动点M从A出发，沿AC以2m/S的速度匀速直线运动到点C，动点N从B出发，沿BD以1m/S的速度匀速直线运动到点D，当M运动到C点时运动停止．若M、N同时出发，问出发几秒钟后，△MON的面积为

1

4

m2？

Answer 1

分析：（1）根据题意，用“一组对边平行且相等的四边形是平行四边形”先判定平行四边形，再用邻边相等证明菱形；
（2）解方程可得OA、OB的长，用勾股定理可求AB，根据“菱形的面积对应对角线积的一半”计算连线面积；
（3）根据点M、N运动过程中与O点的位置关系，分三种情况分别讨论．

解答：（1）证明：∵AO平分∠BAD，AB∥CD
∴∠DAC=∠BAC=∠DCA
∴△ACD是等腰三角形，AD=DC
又∵AB=AD
∴AB=CD，
∴四边形ABCD为平行四边形，
又∵AB=AD，∴?ABCD是菱形；

（2）解：解方程x²-7x+12=0，得
OA=4，OB=3，
利用勾股定理AB=

OA2+OB2

=5，
S_菱形ABCD=

1

2

AC×BD=

1

2

×8×6=24平方米．

（3）解：在第（2）问的条件下，设M、N同时出发x秒钟后，△MON的面积为

1

4

m2，
当点M在OA上时，x≤2，S_△MON=

1

2

（4-2x）（3-x）=

1

4

；
解得x₁=

5- 2

2

，x₂=

5+ 2

2

（大于2，舍去）；
当点M在OC上且点N在OB上时，2＜x＜3，S_△MON=

1

2

（3-x）（2x-4）=

1

4

，
解得x₁=x₂=

5

2

；
当点M在OC上且点N在OD上时，即3≤x≤4，S_△MON=

1

2

（2x-4）（x-3）=

1

4

；
解得x₁=

5+ 2

2

，x₂=

5- 2

2

（小于3，舍去）．
综上所述：M，N出发

5- 2

2

秒，

5

2

秒，

5+ 2

2

秒钟后，△MON的面积为

1

4

m2．

点评：本题考查了菱形的判定方法，菱形的面积计算方法，分类讨论的数学思想．