题目内容
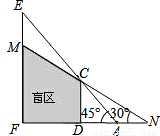
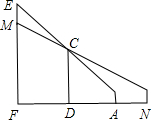如图，CD、EF表示高度不同的两座建筑物，小颖站在A处，正好越过前面建筑物的顶端C看到它后面的建筑物的顶端E，仰角为45°；小颖沿直线FA由点A后移10米到达位置点N，正好看到建筑物EF上的点M，仰角为30°．已知小颖的眼睛距离地面1.5米，CD、EF两座建筑物间的距离为25米，求建筑物CD、EF的高（结果保留根号）．分析：设小颖的头部为K和N，连接NK作FN的平行线交CD，EF于H，W，由已知条件可求出CH，EW分别加上小颖的眼睛距离地面1.5米，即建筑物CD、EF的高．
解答：解：设EW=x米，连接NK，作FN的平行线交CD，EF于H，W，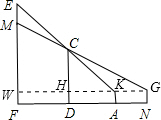
∴∠EKW=45°，∠MGW=30°，
由题意可知：△EWH，△CHK为等腰直角三角形，四边形WHDF，四边形WKAF，四边形KGNA为矩形，
∴WK=WE=x米，
∴HK=WK-WH=（x-25）米，
∴CH=HK=（x-25）米，
∵HGHK+KG=x-25+10=（x-15）米，
∴tan30°=
=
=
，
∴x=（45+5
）米，
∴CD=CH+DH=45+5
-20+1.5=（26.5+5
）米，EF=EW+WF=45+5
+1.5=（46.5+5
）米，
答：建筑物CD、EF的高分别为（26.5+5
）米，（46.5+5
）米．
∴∠EKW=45°，∠MGW=30°，
由题意可知：△EWH，△CHK为等腰直角三角形，四边形WHDF，四边形WKAF，四边形KGNA为矩形，
∴WK=WE=x米，
∴HK=WK-WH=（x-25）米，
∴CH=HK=（x-25）米，
∵HGHK+KG=x-25+10=（x-15）米，
∴tan30°=
| CH |
| HG |
| x-25 |
| x-15 |
| ||
| 3 |
∴x=（45+5
| 3 |
∴CD=CH+DH=45+5
| 3 |
| 3 |
| 3 |
| 3 |
答：建筑物CD、EF的高分别为（26.5+5
| 3 |
| 3 |
点评：本题考查的是解直角三角形的应用，首先构造直角三角形，再借助角边关系、三角函数的定义解题．
练习册系列答案
相关题目
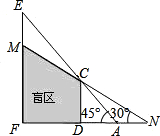如图，CD，EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明延直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，求AN之间的距离．
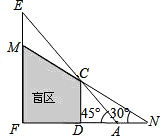如图，CD，EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明延直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，求AN之间的距离．