Question

（1）计算：|1-

3

|+2007⁰+（

1

3

）^-1-2cos30°；
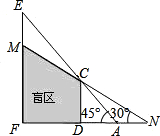
（2）如图，CD，EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明沿直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，求AN之间的距离．

Answer 1

分析：（1）是一道实数的运算，按运算法则计算即可．
（2）主要利用解直角三角形，求出AN的长度即可．

解答：解：（1）原式=-(1-

3

)+1+

1

1 3

-2×

3

2

=-1+

3

+1+3-

3

=3；

（2）由题意可知：∠CDA=90°；
在Rt△CAD中，∠CDA=90°，∠CAD=45°，CD=15，
∴AD=

CD

tan∠CAD

=

15

tan45°

=15．
在Rt△CDN中，∠CDN=90°，∠CND=30°，
∴DN=

CD

tan∠CND

=

15

tan30°

=15

3

．
∴AN=DN-AD=15

3

-15（米）．
故A、N之间的距离为（15

3

-15）米．

点评：第一题难度不大，主要考查学生的运算能力．第二题较复杂，首先要理清AD=CD=15，再利用△CDE中30度角的特殊三角函数求出DN的长，即可求出AN的长．