题目内容
18．分别以2cm、3cm、4cm、5cm的线段为边可构成3个三角形．分析 先确定可以从四条线段中取出三条线段的组数，再根据三角形的三边关系确定能组成三角形的组数．
解答 解：四条线段任意取出三条，可以为：①2、3、4，②2、3、5，③2、4、5，④3、4、5，
①2、3、4可以组成三角形；
②2、3、5，
∵2+3=5，
∴不能组成三角形；
③2、4、5，可以组成三角形；
④3、4、5，可以组成三角形．
故答案为：3．
点评 此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边．
练习册系列答案
相关题目
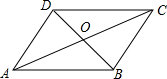如图，在?ABCD中，AB=8，BC=6，对角线AC、BD交于点O，若△AOD的周长为16，则△AOB的周长为18．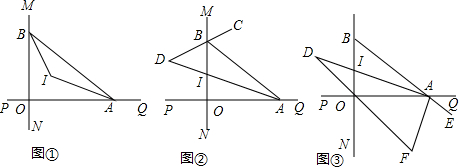
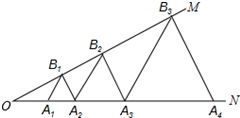13．下列各数中是负数的是（ ）
| A． | |-6| | B． | （-6）-1 | C． | -（-6） | D． | （-6）0 |
如图，已知：∠MON=30°，点A1、A2、A3 在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A6B6A7的边长为32．
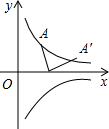反比例函数y=$\frac{2}{x}$（x＞0）和y=-$\frac{2}{x}$（x＞0）的图象如图所示，点A的坐标是（1，2），点B（n，0）是x轴上一个动点，连结AB，将线段BA绕点B顺时针旋转90°得到线段BA′．
7．下列式子成立的是（ ）
| A． | $\frac{1}{ab}$=$\frac{c}{abc}$ | B． | $\frac{x^6}{x^2}$=x3 | C． | $\frac{{a+\frac{1}{2}}}{{a-\frac{1}{2}}}$=$\frac{a+1}{a-1}$ | D． | $\frac{{{a^2}x}}{bx}$=$\frac{a^2}{b}$ |
如图，在六边形ABCDEF中，AF∥CD，AB∥DE，且∠A=120°，∠B=80°，则∠C的度数是160°，∠D的度数120°．