题目内容
8. 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,且∠A=120°,∠B=80°,则∠C的度数是160°,∠D的度数120°.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,且∠A=120°,∠B=80°,则∠C的度数是160°,∠D的度数120°.
分析 连接AC,根据平行线的性质以及三角形的内角和定理,可以求得∠BCD的度数;连接BD,根据平行线的性质和三角形的内角和定理可以求得∠CDE的度数.
解答  解:连接AC.
解:连接AC.
∵AF∥CD,
∴∠ACD=180°-∠CAF,
又∠ACB=180°-∠B-∠BAC,
∴∠BCD=∠ACD+∠ACB=180°-∠CAF+180°-∠B-∠BAC=360°-120°-80°=160°.
连接BD.
∵AB∥DE,
∴∠BDE=180°-∠ABD.
又∵∠BDC=180°-∠BCD-∠CBD,
∴∠CDE=∠BDC+∠BDE=180°-∠ABD+180°-∠BCD-∠CBD=360°-80°-160°=120°.
故答案为:160°,120°.
点评 考查了多边形内角与外角,平行线的性质,本题需要能够熟练运用平行线的性质和三角形的内角和定理进行求解.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | 4x2-3x2=1 | B. | x+x=2x2 | C. | 4x6÷2x2=2x3 | D. | (x2)3=x6 |
3.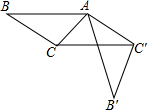 在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
 在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )| A. | 138 | B. | 128 | C. | 118 | D. | 108 |
17.下列图形中,一定能够相似的是( )
| A. | 有一个角为50°的两个等腰三角形 | B. | 邻边之比为1:3的平行四边形 | ||
| C. | 有一个角为30°的两个菱形 | D. | 底角为40°的两等腰梯形 |
