题目内容
3. 如图,直线AA1∥BB1∥CC1,如果$\frac{AB}{BC}=\frac{1}{3}$,AA1=2,CC1=6,那么线段BB1的长是3.
如图,直线AA1∥BB1∥CC1,如果$\frac{AB}{BC}=\frac{1}{3}$,AA1=2,CC1=6,那么线段BB1的长是3.
分析 过A1作AE∥AC,交BB1于D,交CC1于E,得出四边形ABDA1和四边形BCED是平行四边形,求出AA1=BD=CE=2,EC1=6-2=4,$\frac{AB}{BC}$=$\frac{D{A}_{1}}{DE}$=$\frac{1}{3}$,根据BB1∥CC1得出$\frac{D{A}_{1}}{E{A}_{1}}$=$\frac{D{B}_{1}}{E{C}_{1}}$,代入求出DB1=1即可.
解答 解:如图: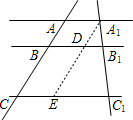
过A1作AE∥AC,交BB1于D,交CC1于E,
∵直线AA1∥BB1∥CC1,
∴四边形ABDA1和四边形BCED是平行四边形,
∴AA1=2,CC1=6,
∴AA1=BD=CE=2,EC1=6-2=4,$\frac{AB}{BC}$=$\frac{D{A}_{1}}{DE}$=$\frac{1}{3}$,
∴∵BB1∥CC1,
∴$\frac{D{A}_{1}}{E{A}_{1}}$=$\frac{D{B}_{1}}{E{C}_{1}}$,
∴$\frac{1}{1+3}$=$\frac{D{B}_{1}}{4}$,
∴DB1=1,
∴BB1=2+1=3,
故答案为:3.
点评 本题考查了平行线分线段成比例定理的应用,能根据定理得出比例式是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,⊙O是△ABC的外接圆,∠AOB=60°,则∠C的度数为( )
如图,⊙O是△ABC的外接圆,∠AOB=60°,则∠C的度数为( )
 如图,⊙O是△ABC的外接圆,∠AOB=60°,则∠C的度数为( )
如图,⊙O是△ABC的外接圆,∠AOB=60°,则∠C的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
11.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有5件不合格,那么你估计该厂这20万件产品中不合格品约为( )
| A. | 1万件 | B. | 2万件 | C. | 19万件 | D. | 20万件 |
18.下列命题是真命题的是( )
| A. | 有一个角相等的两个等腰三角形相似 | |
| B. | 两边对应成比例且有一个角相等的两个三角形相似 | |
| C. | 四个内角都对应相等的两个四边形相似 | |
| D. | 斜边和一条直角边对应成比例的两个直角三角形相似 |
8.下列各点在一次函数y=x+4图象上的是( )
| A. | 点(-7,3) | B. | 点(3,7) | C. | 点(4,-8) | D. | 点(2.5,1.5) |
 如图,P为△ABC中BC边的延长线上一点,∠A=48°,∠B=64,则∠ACP=112°.
如图,P为△ABC中BC边的延长线上一点,∠A=48°,∠B=64,则∠ACP=112°.