题目内容
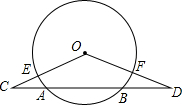 如图,在△COD中,以O为圆心的⊙O与边CD交于A、B两点,与OC、OD两边分别交于点E、F,且CE=DF.?
如图,在△COD中,以O为圆心的⊙O与边CD交于A、B两点,与OC、OD两边分别交于点E、F,且CE=DF.?(1)求证:AC=BD;
(2)若AB=4,tanD=
| ||
| 5 |
考点:垂径定理,解直角三角形
专题:
分析:(1)先根据OE=OF,CE=DF得出OC=OD,过点O作OG⊥AB于点G,则CG=DG,根据垂径定理可得出AG=BG,故可得出结论;
(2)先根据垂径定理求出BG的长,由tanD=
,BD=3得出OG的长,再根据勾股定理求出OB的长即可.
(2)先根据垂径定理求出BG的长,由tanD=
| ||
| 5 |
解答: (1)证明:∵OE=OF,CE=DF,
(1)证明:∵OE=OF,CE=DF,
∴OC=OD.
过点O作OG⊥AB于点G,则CG=DG,AG=BG,
∴CG-AG=DG-BG,即AC=BD;
(2)连接OB,
∵OG⊥A,AB=4,
∴BG=
AB=2.
∵BD=3,tanD=
,
∴DG=BG+BD=2+3=5,
∴
=
=
,
∴OG=
,
在Rt△OGB中,OB=
=
=
.
答:⊙O的半径长是
.
 (1)证明:∵OE=OF,CE=DF,
(1)证明:∵OE=OF,CE=DF,∴OC=OD.
过点O作OG⊥AB于点G,则CG=DG,AG=BG,
∴CG-AG=DG-BG,即AC=BD;
(2)连接OB,
∵OG⊥A,AB=4,
∴BG=
| 1 |
| 2 |
∵BD=3,tanD=
| ||
| 5 |
∴DG=BG+BD=2+3=5,
∴
| OG |
| DG |
| OG |
| 5 |
| ||
| 5 |
∴OG=
| 2 |
在Rt△OGB中,OB=
| OG2+BG2 |
(
|
| 6 |
答:⊙O的半径长是
| 6 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,在△AFC中,B点为AC的中点,E为BD的中点,连接DE、AE,AE交CD于点F,则AF:AE=
如图,在△AFC中,B点为AC的中点,E为BD的中点,连接DE、AE,AE交CD于点F,则AF:AE=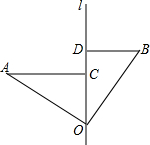 如图,∠AOB=90°,OA=0B,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D,若AC=9,BD=5,则CD=
如图,∠AOB=90°,OA=0B,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D,若AC=9,BD=5,则CD= 两个有理数a、b在数轴上的位置如图所示,则a+b
两个有理数a、b在数轴上的位置如图所示,则a+b