题目内容
10.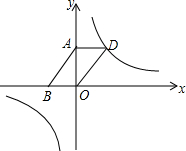 如图,已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象经过?ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0)
如图,已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象经过?ABOD的顶点D,点A、B的坐标分别为(0,3),(-2,0)(1)求出函数解析式;
(2)设点P是该反比例函数图象上的一点,若OD=OP,求P点的坐标.
分析 (1)根据平行四边形的性质和点A、B的坐标,求出点D的坐标,代入解析式计算即可求出m的值,得到函数解析式;
(2)根据反比例函数的对称性,即关于原点对称和关于直线y=x对称,求出P点的坐标.
解答 解:(1)∵四边形ABOC为平行四边形,
∴AD∥OB,AD=OB=2,
而A点坐标为(0,3),
∴D点坐标为(2,3),
∴1-2m=2×3=6,m=-$\frac{5}{2}$,
∴反比例函数解析式为y=$\frac{6}{x}$.
(2)∵反比例函数y=的图象关于原点中心对称,
∴当点P与点D关于原点对称,则OD=OP,此时P点坐标为(-2,-3),
∵反比例函数y=的图象关于直线y=x对称,
∴点P与点D(2,3)关于直线y=x对称时满足OP=OD,此时P点坐标为(3,2),
点(3,2)关于原点的对称点也满足OP=OD,此时P点坐标为(-3,-2),
综上所述,P点的坐标为(-2,-3),(3,2),(-3,-2).
点评 本题考查的是反比例函数图象上点的坐标特征和平行四边形的性质,正确运用平行四边形的性质求出点D的坐标是解题的关键,注意数形结合思想的正确运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.某中学七年级学生共280人,其中男生120人,女生160人.该校对七年级所有学生进行了一次体育测试,并随机抽取了30名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表:
(1)根据表中信息填空:a=7,b=28,m=10%;
(2)从上表的“频数”,“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校七年级体育测试成绩不及格的人数.
| 成绩 | 频数 | 百分比 |
| 不及格 | a | m |
| 及格 | 14 | 20% |
| 良好 | b | 40% |
| 优秀 | 21 | 30% |
| 合计 | 70 | 100% |
(2)从上表的“频数”,“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校七年级体育测试成绩不及格的人数.
15.下列事件是随机事件的是( )
| A. | 没有水分,种子发芽 | B. | 367人中至少有2人的生日相同 | ||
| C. | 三角形的内角和是180° | D. | 小华一出门上学,天就下雨 |
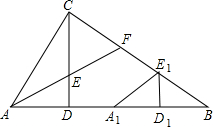 在Rt△ABC中,∠C=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F.
在Rt△ABC中,∠C=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F.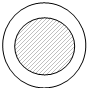 如图所示,航空兵一定能把物资投到指定的区域(大圆)内,但落在中心区域小圆(阴影部分)的概率为$\frac{1}{2}$,则小圆与大圆半径之比为$\frac{\sqrt{2}}{2}$.
如图所示,航空兵一定能把物资投到指定的区域(大圆)内,但落在中心区域小圆(阴影部分)的概率为$\frac{1}{2}$,则小圆与大圆半径之比为$\frac{\sqrt{2}}{2}$.