Question

【题目】已知抛物线与直线交于，B两点，与y轴交于点．

（1）求抛物线的解析式；

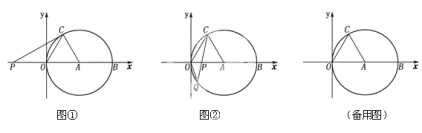
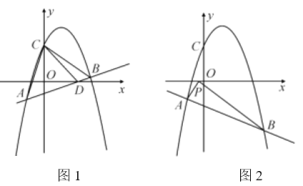
（2）如图1，直线AB交轴于点D，且，求点B的坐标；

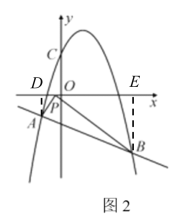
（3）如图2，当时，在x轴上有且只有一点P，使，求k的值．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据待定系数法求解即可；

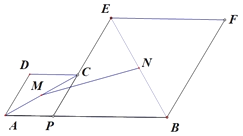
（2）由推出AC=AD，过点A作轴于点M，轴于点N，证明，得到，从而得到AB的解析式，联立二次函数和一次函数，可得点B坐标；

（3）分别过A，B两点作轴于点D，轴于点E，证明，则，设AB解析式为，联立，解出，得到点B坐标，设，代入，再令判别式为零，解出k值即可.

解：（1）抛物线与直线交于，B两点，与y轴交于点C（0，2），

∴c=2，将A（-1，-1）代入，

解得：b=2，

∴抛物线的表达式为：；

（2）∵，

∴，即，

∴，

过点A作轴于点M，轴于点N，

∴，

∴，

∴，

∴，

∴，

∴AB的解析式为，

联立，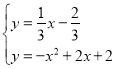

解得：，（舍），

可求；

（3）分别过A，B两点作轴于点D，轴于点E，

∵∠APB=90°，

∴∠APD+∠BPE=90°，而∠APD+∠PAD=90°，

∴∠BPE=∠PAD，而∠ADP=∠BEP，

则，

∴，

设AB解析式为，

联立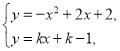

∴，

∴，，

设，则，

∴，当轴上只有唯一点P时，，

∴，

∴（舍），．