题目内容

13．抛物线y=-3x2-x+4与x轴交点的个数是（　　）
A．0B．1C．2D．3

分析 令y=0，则得到关于x的一元二次方程y=-3x2-x+4，根据根的判别式判断有几个解就是该抛物线与x轴有几个交点．

解答 解：当与x轴相交时，函数值为0．即-3x2-x+4=0，
△=b2-4ac=（-1）2-4×（-3）×4=49＞0，
∴有2个不相等的实数根，
∴抛物线y=-3x2-x+4与x轴有2个交点，
故选：C．

点评 本题考查了抛物线与x轴的交点．x轴上的点的纵坐标为0；抛物线与x轴的交点个数与函数值为0的一元二次方程的解的个数相同．

练习册系列答案
相关题目
3．若$\sqrt{32n+16}$是正整数，则正整数n的最小值为4．
4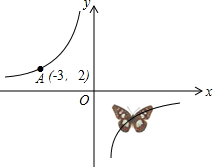．如图，反比例函数y=$\frac{k}{x}$（k≠0，k是常数）的图象经过A点，则该函数图象上被蝴蝶遮住的点的坐标可能是（　　）
A．（-2，3）B．（2，-2）C．（-1，6）D．（2，-3）
1．如图，AE是△ABC的角平分线，ED平分∠AEB且垂直AB
（1）若∠C=75°，求∠B的度数；
（2）若∠AEC=∠C，求∠B的度数．
8．直接写出答案
（1）（-2.8）+（+1.9）=-0.9，
（2）0.75-（-3$\frac{1}{4}$）=4，
（3）0-（-12.19）=12.19，
（4）|-3|-（-2）=5，
（5）32-（-2）2=5，
（6）（-$\frac{1}{2}$）99×（-2）100=-2．
17．如果收入10.5元表示为+10.5元，那么支出6元可表示为-6元．
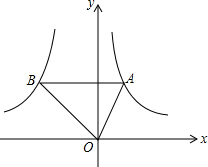4．如图，点A是反比例函数y1=$\frac{2}{x}$（x＞0）图象上的任意一点，过点A作  AB∥x轴，交另一个比例函数y2=$\frac{k}{x}$（k＜0，x＜0）的图象于点B．
（1）若S△AOB的面积等于3，则k是=-4；
（2）当k=-8时，若点A的横坐标是1，求∠AOB的度数；
（3）若不论点A在何处，反比例函数y2=$\frac{k}{x}$（k＜0，x＜0）图象上总存在一点D，使得四边形AOBD为平行四边形，求k的值．
20．数与数的关系有时真奇妙，例如，2+2=2×2，3+$\frac{3}{2}$=3×$\frac{3}{2}$，即两个数的和恰好等于它们的积．
（1）猜想：按此规律，第3个等式应该是：4+$\frac{4}{3}$=4×$\frac{4}{3}$；n个等式应该是：n+$\frac{n}{n-1}$=n×$\frac{n}{n-1}$；
（2）拓展：n能否改为其它实数呢？
当n=$\frac{1}{2}$时，上述等式为：$\frac{1}{2}$+（-1）=$\frac{1}{2}×（-1）$；当n=-2时，上述等式为：-2+$\frac{2}{3}$=（-2）×$\frac{2}{3}$；
（3）若设满足该规律的两数为a和b（ab≠0），试证明a、b满足关系式．$\frac{1}{a}$+$\frac{1}{b}$=1．
20．下列因式分解中，正确的是（　　）
A．x2-9=（x-3）2B．3a-3b+3=3（a-b）
C．-x2+2xy-y2=-（x-y）2D．a2-3a-4=（a+2）（a-2）-3a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网