题目内容
【题目】(概念认知):
城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A(![]() ,
,![]() )和B(
)和B(![]() ,
,![]() ),用以下方式定义两点间距离:d(A,B)=
),用以下方式定义两点间距离:d(A,B)=![]() +
+![]() .
.
(数学理解):
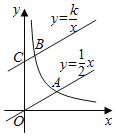
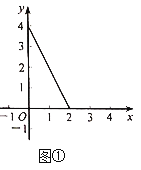
(1)①已知点A(﹣2,1),则d(O,A)= ;②函数![]() (0≤x≤2)的图像如图①所示,B是图像上一点,d(O,B)=3,则点B的坐标是 .
(0≤x≤2)的图像如图①所示,B是图像上一点,d(O,B)=3,则点B的坐标是 .
(2)函数![]() (x>0)的图像如图②所示,求证:该函数的图像上不存在点C,使d(O,C)=3.
(x>0)的图像如图②所示,求证:该函数的图像上不存在点C,使d(O,C)=3.

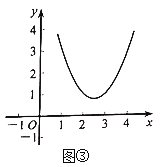
(3)函数![]() (x≥0)的图像如图③所示,D是图像上一点,求d(O,D)的最小值及对应的点D的坐标.
(x≥0)的图像如图③所示,D是图像上一点,求d(O,D)的最小值及对应的点D的坐标.
(问题解决):
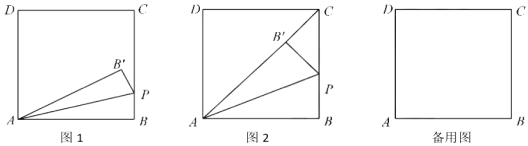
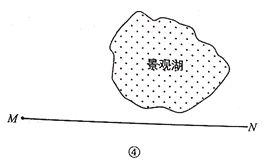
(4)某市要修建一条通往景观湖的道路,如图④,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边,如何修建能使道路最短?(要求:建立适当的平面直角坐标系,画出示意图并简要说明理由)
【答案】(1)【数学理解】:① 3, ② (1,2) ;(2)见解析;(3)![]() 有最小值3,此时点
有最小值3,此时点![]() 的坐标是(2,1);【问题解决】:(4)先沿
的坐标是(2,1);【问题解决】:(4)先沿![]() 方向修建到
方向修建到![]() 处,再沿
处,再沿![]() 方向修建到
方向修建到![]() 处,见解析.
处,见解析.
【解析】
(1)①根据定义可求出d(O,A)=|0+2|+|01|=2+1=3;②由两点间距离:d(A,B)=|x1x2|+|y1y2|及点B是函数y=2x+4的图象上的一点,可得出方程组,解方程组即可求出点B的坐标;
(2)由条件知x>0,根据题意得![]() ,整理得x23x+4=0,由△<0可证得该函数的图象上不存在点C,使d(O,C)=3.
,整理得x23x+4=0,由△<0可证得该函数的图象上不存在点C,使d(O,C)=3.
(3)根据条件可得|x|+|x25x+7|,去绝对值后由二次函数的性质可求出最小值;
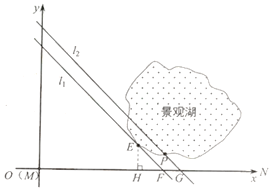
(4)以M为原点,MN所在的直线为x轴建立平面直角坐标系xOy,将函数y=x的图象沿y轴正方向平移,直到与景观湖边界所在曲线有交点时停止,设交点为E,过点E作EH⊥MN,垂足为H,修建方案是:先沿MN方向修建到H处,再沿HE方向修建到E处,可由d(O,P)≥d(O,E)证明结论即可.
解:(1)①由题意得:d(O,A)=|0+2|+|01|=2+1=3;
②设B(x,y),由定义两点间的距离可得:|0x|+|0y|=3,
∵0≤x≤2,
∴x+y=3,
∴![]() ,
,
解得: x=1,y=2,
∴B(1,2),
(2)假设函数![]() 的图像上存在点
的图像上存在点![]() ,使
,使![]() .
.
根据题意,得![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() .
.
方程两边乘![]() ,得
,得![]() .
.
整理,得![]() .
.
因为![]() ,
,
所以方程![]() 无实数根.
无实数根.
所以函数![]() 的图像上不存在点
的图像上不存在点![]() ,使
,使![]() .
.
(3)设![]() .
.
根据题意,得![]() .
.
因为![]() ,又
,又![]() ,
,
所以![]() .
.
所以当![]() 时,
时,![]() 有最小值3,此时点
有最小值3,此时点![]() 的坐标是
的坐标是![]() .
.
(4)如图,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() .将函数
.将函数![]() 的图像沿
的图像沿![]() 轴正方向平移.直到与景观湖边界所在曲线有交点时停止.设交点为
轴正方向平移.直到与景观湖边界所在曲线有交点时停止.设交点为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .修建方案是:先沿
.修建方案是:先沿![]() 方向修建到
方向修建到![]() 处,再沿
处,再沿![]() 方向修建到
方向修建到![]() 处.
处.
理由:设过点![]() 的直线
的直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .在景观湖边界所在曲线上任取一点
.在景观湖边界所在曲线上任取一点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .因为
.因为![]() ,所以
,所以![]() .同理
.同理![]() .因为
.因为![]() ,所以
,所以![]() .因此,上述方案修建的道路最短.
.因此,上述方案修建的道路最短.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
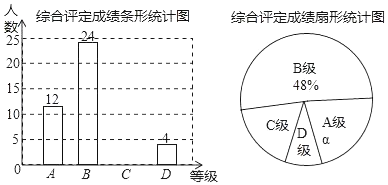
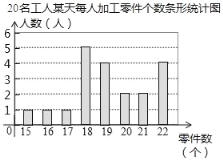
暑假接力赛新疆青少年出版社系列答案【题目】某部门为了解工人的生产能力情况,进行了抽样调查.该部门随机抽取了20名工人某天每人加工零件的个数,数据如下:整理上面数据,得到条形统计图;样本数据的平均数、众数、中位数如表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 19.2 | m | n |
根据以上信息,解答下列问题:
(1)上表中m、n的值分别为 , ;
(2)为调动积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让60%左右的工人能获奖,应根据 来确定奖励标准比较合适(填“平均数”、“众数”或“中位数”);
(3)该部门规定:每天加工零件的个数达到或超过21个的工人为生产能手若该部门有300名工人,试估计该部门生产能手的人数;
(4)现决定从小王、小张、小李、小刘中选两人参加业务能手比赛,直接写出恰好选中小张、小李两人的概率.
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
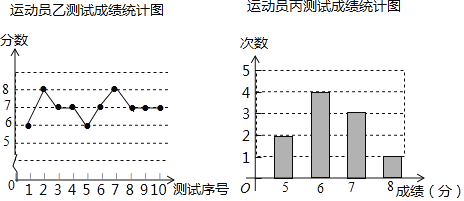
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)