题目内容
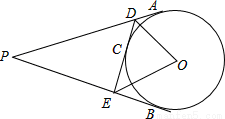
如图所示,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD= .
.

(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
(1)证明见解析;(2)2 -
- .
.
【解析】
试题分析:(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;
(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
试题解析:(1)证明:连接OC.

∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°-∠A-∠D-∠2=90°.
∴CD是⊙O的切线.
(2)【解析】
∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC= .
.
在Rt△OCD中,
∵ =tan60°,
=tan60°,
∴CD=2 .
.
∴SRt△OCD= OC×CD=
OC×CD= ×2×2
×2×2 =2
=2 .
.
∴图中阴影部分的面积为:2 -
- .
.
考点:1.扇形面积的计算;2.等腰三角形的性质;3.切线的判定;4.特殊角的三角函数值.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
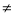 x2有下列结论:①x1=2,x2=3;②m>
x2有下列结论:①x1=2,x2=3;②m>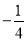 ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是__________(填正确结论的序号)
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是__________(填正确结论的序号)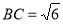 ,AC=3,则CD长为( )
,AC=3,则CD长为( )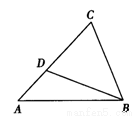
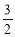 C.2 D.
C.2 D.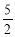
 B.
B. C.
C. D.
D.
 是一元二次方程,则m= ;
是一元二次方程,则m= ; ,AB=4,tan∠ACD=
,AB=4,tan∠ACD=