Question

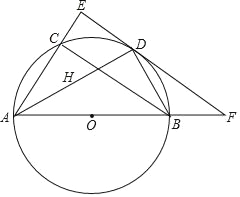
【题目】如图，四边形内接于，，是对角线。点E在的延长线上，且．

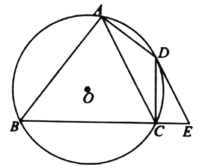
（1）判断与的位置关系，并说明理由；

（2）与的延长线交于点F，若，，，求的长．

Answer 1

【答案】（1）DE与相切，理由见详解；（2）

【解析】

(1)连接BD，由，可知BD是直径，根据等量代换和圆周角定理，可得：∠BDC+∠CDE=90°，进而，可得到结论；

(2)设AF=x，易证：FAD~FCB，则，，推出CF=2x，DF =2x-2，根据勾股定理，列出方程，即可求解.

（1） 连接BD，

∵，

∴BD是直径，

∴∠BCD=90°，

∴∠DEC+∠CDE=90°，

∵，

∴∠BAC+∠CDE=90°,

∵∠BAC=∠BDC，

∴∠BDC+∠CDE=90°，即：∠BDE=90°，

∴BD⊥DE，

∵点D在上，

∴DE与相切.

（2）设AF=x，

∵，BD⊥DE，

∴BD⊥AC，

∴AD=CD=2，AB=CB=4，

∵四边形内接于，

∴∠FAD=∠FCB，

∵∠F=∠F，

∴FAD~FCB，

∴，即：，

∴CF=2x，

∴DF=CF-CD=2x-2，

∵，

∴∠DAF=90°，

∴，

∴，解得：，（舍去），

∴AF=.