题目内容
16.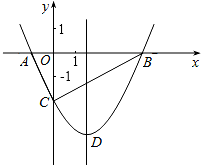 如图,抛物线y=$\frac{1}{2}{x}^{2}$-$\frac{3}{2}x-2$与x轴交于A、B两点,与y轴交于C点,点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,则m的值为$\frac{24}{41}$.
如图,抛物线y=$\frac{1}{2}{x}^{2}$-$\frac{3}{2}x-2$与x轴交于A、B两点,与y轴交于C点,点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,则m的值为$\frac{24}{41}$.
分析 作点C关于x轴的对称点E,连接ED于x轴交于点M,则点M即为所求,根据两点之间线段最短,从而可以解答本题.
解答 解:∵抛物线y=$\frac{1}{2}{x}^{2}$-$\frac{3}{2}x-2$,
∴将x=0代入抛物线y=$\frac{1}{2}{x}^{2}$-$\frac{3}{2}x-2$得,y=-2;抛物线y=$\frac{1}{2}{x}^{2}$-$\frac{3}{2}x-2$=$\frac{1}{2}(x-\frac{3}{2})^{2}-\frac{25}{8}$.
∵抛物线y=$\frac{1}{2}{x}^{2}$-$\frac{3}{2}x-2$与y轴交于C点,顶点为D点,
∴点C的坐标为(0,-2),点D的坐标为($\frac{3}{2},-\frac{25}{8}$).
∵点M(m,0)是x轴上的一个动点,
如下图所示:
作点C关于x轴的对称点点E,连接DE与x轴交于点M,则点M即为所求.
设过点E(0,2)D($\frac{3}{2},-\frac{25}{8}$)的直线的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{b=2}\\{\frac{3}{2}k+b=-\frac{25}{8}}\end{array}\right.$
解得,$a=-\frac{41}{12}$,b=2.
∴$y=-\frac{41}{12}x+2$.
令y=0,则$0=-\frac{41}{12}x+2$,得x=$\frac{24}{41}$.
∴当MC+MD的值最小时,则m的值为$\frac{24}{41}$.
故答案为:$\frac{24}{41}$.
点评 本题考查轴对称--最短路径问题、求直线的解析式,关键是找出所求问题需要的条件,灵活变化.

 阅读快车系列答案
阅读快车系列答案| A. | -2(a-1)=-2a-1 | B. | -2(a-1)=-2a+1 | C. | -2(a-1)=-2a-2 | D. | -2(a-1)=-2a+2 |
| A. |  | B. |  | C. |  | D. |  |
| A. | a=3,b=6,c=2,d=4 | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{6}$,d=$\sqrt{3}$ | ||
| C. | a=4,b=6,c=5,d=10 | D. | a=2,b=2$\sqrt{3}$,c=$\sqrt{5}$,d=$\sqrt{15}$ |
①单项式-$\frac{2{x}^{2}y}{5}$的系数是-2,次数是3;
②-5π,0.333…都是无理数;
③在-(-8),|-1|,-|0|,(-2)3这四个数中,非负数共有3个;
④平方等于本身数只有0和1.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | -3 | B. | +3 | C. | $\frac{1}{3}$ | D. | -0.3 |
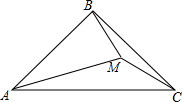 如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30°
如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30°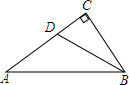 如图,△ABC,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,求CD的长.
如图,△ABC,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,求CD的长.