题目内容
【题目】如图1,在边长为4的菱形ABCD中,AC为其对角线,∠ABC=60°点M、N分别是边BC、边CD上的动点,且MB=NC.连接AM、AN、MN.MN交AC于点P.

(1)△AMN是什么特殊的三角形?说明理由.并求其面积最小值;
(2)求点P到直线CD距离的最大值;

(3)如图2,已知MB=NC=1,点E、F分别是边AM、边AN上的动点,连接EF、PF,EF+PF是否存在最小值?若存在,求出最小值及此时AE、AF的长;若不存在,请说明理由.
【答案】(1)△AMN为等边三角形,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)△AMN是等边三角形,AM⊥BC时面积最小.只要证明△AMB≌△ANC,推出AM=AN,∠BAM=∠CAN即可解决问题.
(2)如图2中,当AM⊥BC时,点P到CD距离最大.作PE⊥CD于E.
(3)如图3中,作点P关于AN的对称点为K,过点K做AM的垂线,交AN为F,交AM为E,此时,EF+PF最短,连接AK、作AG⊥MN于G,MH⊥AB于H.首先求出AM、AG的长,再证明△AGP≌△KEA,推出KE=AG即可.
解:(1)△AMN为等边三角形;
如图1中,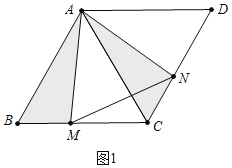
∵ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形
在△AMB和△ANC中,
AB=AC
∠B=∠ACN=60°
BM=NC
∴△AMB≌△ANC
∴AM=AN,∠BAM+∠MAC=∠MAC+∠NAC=60°,
∴∠MAN=60°,
∴△AMN为等边三角形,
当AM⊥BC时,△AMN的边长最小,面积最小,
此时AM=MN=AN=![]()
(2)如图2中,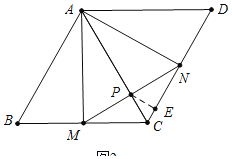
当AM⊥BC时,点P到CD距离最大.作PE⊥CD于E.
理由:由(1)可知△AMN是等边三角形,
当AM⊥BC时,△AMN的边长最小,此时PA长最小,PC的长最大,点P到直线CD距离的最大,
∵BM=MC=2,∠CMP=30°,∠MPC=90°,
∴PC=![]() MC=1,
MC=1,
在Rt△PCE中,∵∠CPE=30°,PC=1,
∴EC=![]() PC=
PC=![]() ,
,
∴PE=![]() .
.
∴点P到直线CD距离的最大值为![]() ;
;
(3)如图3中,作点P关于AN的对称点为K,过点K做AM的垂线,交AN为F,交AM为E,此时,EF+PF最短,由于对称,PF=KF,EF为垂线段(垂线段最短).
连接AK、作AG⊥MN于G,MH⊥AB于H.
在Rt△BMH中,∵BM=1,∠BMH=30°,
∴BH=![]() ,HM=
,HM=![]() ,
,
∴![]() ,
,
∵△AMN是等边三角形,
∴AG=![]() .
.
∵∠APG=∠PCM+∠PMC=60°+∠PMC,
∵∠PMC+∠PCM+∠CPM=180°,∠NAP+∠ANP+∠APN=180°,∠ANP=∠PCM=60°,∠APN=∠CPM,
∴∠CMP=∠NAP=∠NAK,
∵∠EAK=∠EAN+∠NAK=60°+∠NAK,
∴∠APG=∠EAK,
∵∠AGP=∠AEK=90°,AP=AK,
∴△AGP≌△KEA,
∴KE=AG=![]() .
.
∴EF+PF的最小值为![]() ,
,
∵∠PCN=∠PCM,
∴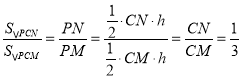 ,
,
∴PN=![]() ,
,
∴AE=PG=GN-PN=![]() ,
,
∵在Rt△AFE中,∠AFE=30°,∴AF=2AE,
∴AF=![]() .
.

 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】平价大药房准备购进![]() 、一次性医用两种口罩.两种口罩的进价和售价如表.已知:用
、一次性医用两种口罩.两种口罩的进价和售价如表.已知:用![]() 元购进一次性医用口罩的数量是用
元购进一次性医用口罩的数量是用![]() 元购进
元购进![]() 口罩的数量的
口罩的数量的![]() 倍.
倍.
| 一次性医用口罩 | |
进价(元 |
|
|
售价(元 |
|
|
(1)求![]() 的值;
的值;
(2)要使购进的![]() 、一次性医用两种口罩共
、一次性医用两种口罩共![]() 个的总利润不少于
个的总利润不少于![]() 元,且不超过
元,且不超过![]() 元,问该药店共有多少种进货方案?
元,问该药店共有多少种进货方案?





