题目内容
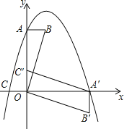
在平面直角坐标系中,平行四边形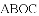
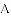

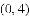
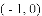
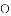
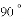 ,得到平行四边形
,得到平行四边形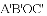

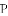

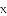
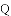
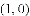
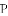

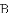
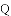
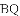
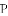
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目


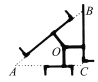
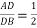 ,则下列结论中正确的是( )
,则下列结论中正确的是( )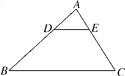
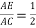 B.
B. 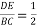 C.
C.  D.
D. 
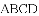
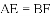
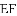
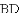
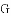
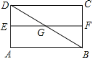
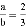 ,则
,则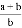 的值是( )
的值是( ) B.
B.  C.
C.  D.
D. 
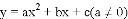 的图象的一部分,给出下列命题:①
的图象的一部分,给出下列命题:①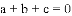
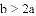
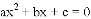 的两根分别为
的两根分别为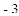
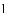
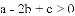
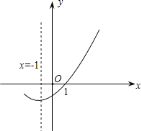
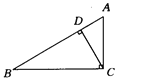
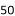

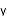
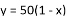
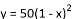 C.
C. 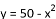 D.
D.