题目内容
把矩形纸片ABCD折叠，使B、C两点恰好落在AD边上的点P处（如图），若∠MPN=90°，PM=6cm，PN=8cm，那么矩形纸片ABCD的宽为________cm，面积为________cm2．
4.8 115.2
分析：根据勾股定理，得MN=10；根据直角三角形的面积公式，得AB=4.8；根据折叠，知BC=6+8+10=24，进而求得矩形的面积．
解答：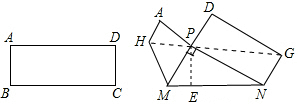
解：过点P作PE⊥MN，
∵∠MPN=90°，PM=6cm，PN=8cm，
∴MN=
=10（cm），
∴S△PMN=
PM•PN=MN•PE，
∴PM•PN=MN•PE，
即PE=
=4.8（cm），
即矩形纸片ABCD的宽为：4.8cm；
∵BC=PM+MN+PN=6+10+8=24（cm），
∴S矩形ABCD=4.8×24=115.2（cm2）．
故答案为：4.8，115.2．
点评：此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法．此题难度适中，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想的应用．
分析：根据勾股定理，得MN=10；根据直角三角形的面积公式，得AB=4.8；根据折叠，知BC=6+8+10=24，进而求得矩形的面积．
解答：
解：过点P作PE⊥MN，∵∠MPN=90°，PM=6cm，PN=8cm，
∴MN=
=10（cm），∴S△PMN=
PM•PN=MN•PE，∴PM•PN=MN•PE，
即PE=
=4.8（cm），即矩形纸片ABCD的宽为：4.8cm；
∵BC=PM+MN+PN=6+10+8=24（cm），
∴S矩形ABCD=4.8×24=115.2（cm2）．
故答案为：4.8，115.2．
点评：此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法．此题难度适中，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
24、小明打算用如图的矩形纸片ABCD折出一个等边三角形．他的操作步骤是：
17、如图，把矩形纸片ABCD沿BD对折，使C落在E处，BE与AD相交于O，写出一组相等的线段
如图，四边形ABCD是矩形纸片．
把矩形纸片ABCD沿BE折叠，使得BA边与BC重合，然后再沿着BF折叠，使得折痕BE也与BC边重合，展开后如图所示，则∠DFB等于（ ）| A、22.5° | B、67.5° | C、112.5° | D、120° |
在一次探究学习活动中，把矩形纸片ABCD折叠，使得顶点A与边BC的动点P重合（P不与点B、C重合），EF为折痕，点F，E分别在边CD，AB上，连接AE，EP，PA，EF与PA相交于点G．