题目内容

已知实数a，b在数轴上的位置如图所示：试化简
(a+
3
)2
-
(b-2
3
)2
-
a2-2ab+b2
．
分析：根据数轴得出-3＜a＜-2，4＜b＜5，推出a＜-
3
，b＞2
3
，a-b＜0，根据二次根式的性质得出|a+
3
|-|b-2
3
|-|a-b|，推出-（a+
3
）-（b-2
3
）-[-（a-b）]，求出即可．
解答：解：根据数轴可知：-3＜a＜-2，4＜b＜5，
∴a＜-
3
，b＞2
3
，a-b＜0，
∴
(a+
3
)2
-
(b-2
3
)2
-
a2-2ab+b2

=|a+
3
|-|b-2
3
|-|a-b|
=-（a+
3
）-（b-2
3
）-[-（a-b）]
=-a-
3
-b+2
3
+a-b
=
3
-2b．
点评：本题考查了绝对值，二次根式的性质的应用，关键是根据数轴和二次根式的性质得出|a+
3
|-|b-2
3
|-|a-b|和-（a+
3
）-（b-2
3
）-[-（a-b）]，题目比较典型，但是一道比较容易出错的题目．
练习册系列答案
相关题目
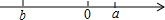精英家教网已知实数a、b在数轴上的位置如图所示，则以下三个命题：（1）a3-ab2＜0，（2）
(a+b)2
=a+b，（3）
1
a-b
＜
1
a
，其中真命题的序号为
 
．
21、已知实数a、b在数轴上的对应点如图所示，则下列命题中正确的是（　　）
已知实数a，b在数轴上对应位置如图所示，则
a2+2ab+b2
-
b2
=
 
．
精英家教网
（2013•滨湖区一模）已知实数a、b在数轴上的位置如图所示，则下列等式成立的是（　　）
已知实数a、b在数轴上的位置如图所示，化简|a+b|-
(a-b)2
的结果为
-2a
-2a
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网