Question

【题目】如图，在中，，，，点分别是边的中点，连接．将绕点顺时针方向旋转，记旋转角为．

①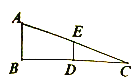 ②

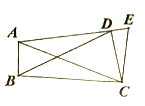③ ④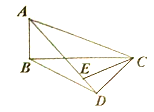

（1）问题发现：当时， ．

（2）拓展探究：试判断：当时，的大小有无变化？请仅就图②的情况给出证明．

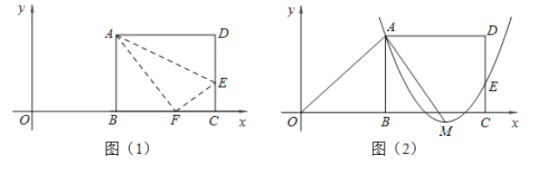
（3）问题解决：当旋转至三点共线时，如图③，图④，直接写出线段的长．

Answer 1

【答案】（1）；（2）无变化，理由见解析；（3）图③中；图④中；

【解析】

（1）问题发现：由勾股定理可求AC的长，由中点的性质可求AE，BD的长，即可求解；

（2）拓展探究：通过证明△ACE∽△BCD，可得；

（3）问题解决：由三角形中位线定理可求DE=1，∠EDC=∠B=90°，由勾股定理可求AD的长，即可求AE的长．

解：（1）问题发现：

∵∠B=90°，AB=2，BC=6，

∴AC=，

∵点D，E分别是边BC，AC的中点，

∴AE=EC=，BD=CD=3，

∴，

故答案为：；

（2）无变化；证明如下：

∵点，分别是边，的中点，

∴由旋转的性质，，，

∵，，

∴，

∴，

∴；

（3）如图③，

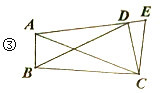
∵点D，E分别是边BC，AC的中点，

∴DE=AB=1，DE∥AB，

∴∠CDE=∠B=90°，

∵将△EDC绕点C顺时针方向旋转，

∴∠CDE=90°=∠ADC，

∴AD=，

∴AE=AD+DE=；

如图④，

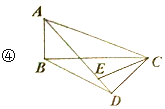
由上述可知：AD=，

∴；