题目内容
1. 如图,在Rt△ABC中,CD是斜边AB上的中线,已知AC=8,sinB=$\frac{4}{5}$,则CD=5.
如图,在Rt△ABC中,CD是斜边AB上的中线,已知AC=8,sinB=$\frac{4}{5}$,则CD=5.
分析 在Rt△ACB中,根据三角函数的定义可求出AB,然后根据直角三角形斜边上的中线等于斜边的一半,就可求出CD的值.
解答 解:在Rt△ACB中,sinB=$\frac{AC}{AB}$=$\frac{8}{AB}$=$\frac{4}{5}$,
∴AB=10.
∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=$\frac{1}{2}$AB=5.
故答案为5.
点评 本题主要考查了三角函数的定义、直角三角形斜边上的中线等于斜边的一半等知识,突出了对基础知识的考查.

练习册系列答案
相关题目
11.下列四个数中,在-2到0之间的数是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.现以点O为坐标原点,在网格中建立如图所示的平面直角坐标系.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.现以点O为坐标原点,在网格中建立如图所示的平面直角坐标系. 如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧$\widehat{AC}$的长度为$\frac{4π}{5}$.
如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧$\widehat{AC}$的长度为$\frac{4π}{5}$.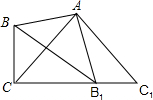 如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
如图所示,∠BAB1=∠CAC1=90°,AB=AB1,AC=AC1,B1在CC1上.
 如图所示,已知AD是Rt△ABC的斜边BC上的高,E为AC上一点,连接BE交AD于点F,若AE=AF,求证:BE平分∠ABC.
如图所示,已知AD是Rt△ABC的斜边BC上的高,E为AC上一点,连接BE交AD于点F,若AE=AF,求证:BE平分∠ABC.