题目内容
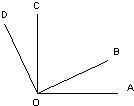
 如图,OA⊥OC,OB⊥OD,下列结论不正确的是
如图,OA⊥OC,OB⊥OD,下列结论不正确的是
- A.∠AOB=∠COD
- B.∠BOC+∠AOD=180°
- C.∠AOB+∠COD=90°
- D.∠AOB+∠BOC=90°
C
分析:因为OA⊥OC,OB⊥OD,而且共一个顶点,所以∠AOC=∠BOD=90°,即∠AOB+∠BOC=∠COD+∠BOC=90度.再分析选项得到正确答案.
解答:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD、∠BOC+∠AOD=180°、∠AOB+∠BOC=90°.
故选C.
点评:本题是角的计算,考查了有公共部分的直角的特点.根据其特点得出正确结论.
分析:因为OA⊥OC,OB⊥OD,而且共一个顶点,所以∠AOC=∠BOD=90°,即∠AOB+∠BOC=∠COD+∠BOC=90度.再分析选项得到正确答案.
解答:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD、∠BOC+∠AOD=180°、∠AOB+∠BOC=90°.
故选C.
点评:本题是角的计算,考查了有公共部分的直角的特点.根据其特点得出正确结论.

练习册系列答案
相关题目

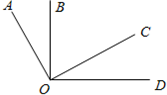 9、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( )
9、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( ) 已知:如图,OA=OC,OB=OD,试说明:△AOB≌△COD.
已知:如图,OA=OC,OB=OD,试说明:△AOB≌△COD. 8、如图,OA=OC,OB=OD,则图中全等三角形共有
8、如图,OA=OC,OB=OD,则图中全等三角形共有 10、如图,OA⊥OC,OB⊥OD,∠BOC=35°,则∠AOD=
10、如图,OA⊥OC,OB⊥OD,∠BOC=35°,则∠AOD=