题目内容
16. 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB,直线y=mx-m恒过定点,且与AB有交点,求m的取值范围$\frac{3}{5}$≤m≤3.
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB,直线y=mx-m恒过定点,且与AB有交点,求m的取值范围$\frac{3}{5}$≤m≤3.
分析 由y=mx-m=m(x-1),令x-1=0,y=0,从而求得直线y=mx-m恒过定点(1,0),然后把A(2,3)、B(6,3),分别代入y=mx-m求得的m值,从而求得m的取值.
解答 解:∵y=mx-m=m(x-1),
∴x-1=0,即x=1时,y=0,
∴直线y=mx-m恒过定点(1,0),
把A(2,3)代入y=mx-m,得3=2m-m
∴m=3,
把B(6,3)代入y=mx-m,得3=6m-m
∴m=$\frac{3}{5}$,
∴m的取值范围是$\frac{3}{5}$≤m≤3.
故答案为$\frac{3}{5}$≤m≤3.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
7.已知a2-a=7,则代数式$\frac{a-1}{a+2}$•$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$÷$\frac{1}{{a}^{2}-1}$的值是( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | 5 |
 如图所示,DE是△ABC的中位线,DE=3,则BC=6.
如图所示,DE是△ABC的中位线,DE=3,则BC=6.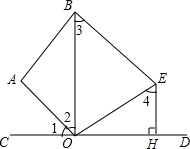 如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.
如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.