题目内容
 在△ABC中,∠A=60°,AB=10,AC=8,⊙O与边AB,AC相切,设⊙O与边AB相切的点为E.
在△ABC中,∠A=60°,AB=10,AC=8,⊙O与边AB,AC相切,设⊙O与边AB相切的点为E.(1)求⊙O的半径R与EA的长x之间的函数关系式;
(2)求当⊙O与△ABC三边相切时,⊙O的半径R;
(3)若⊙O在变化过程中都是落在△ABC内(含相切)时,写出x的取值范围.
考点:圆的综合题
专题:综合题
分析:(1)设⊙O与边AC相切于点F,连接OA、OE、OF,如图1,根据切线的性质可得∠AEO=90°,根据切线长定理可得∠EAO=30°,然后在Rt△AEO中运用三角函数就可解决问题;
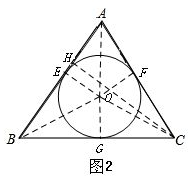
(2)过点C作CH⊥AB于H,设⊙O与边BC相切于点G,连接OG,OA、OB、OC,如图2,在Rt△AHC中运用三角函数可求出HC、AH,然后在Rt△BHC中运用勾股定理可求出BC,然后运用等积变换就可求出⊙O的半径;
(3)只需先求出临界位置(⊙O与△ABC三边相切)时对应的x的值,就可解决问题.
(2)过点C作CH⊥AB于H,设⊙O与边BC相切于点G,连接OG,OA、OB、OC,如图2,在Rt△AHC中运用三角函数可求出HC、AH,然后在Rt△BHC中运用勾股定理可求出BC,然后运用等积变换就可求出⊙O的半径;
(3)只需先求出临界位置(⊙O与△ABC三边相切)时对应的x的值,就可解决问题.
解答:解:(1)设⊙O与边AC相切于点F,连接OA、OE、OF,如图1.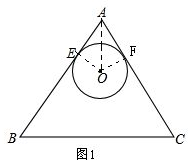
根据切线的性质可得:∠AEO=∠AFO=90°,
根据切线长定理可得:∠EAO=∠FAO=
∠BAC=30°.
在Rt△AEO中,
tan∠EAO=
=
=
,
∴R=
x,
则⊙O的半径R与EA的长x之间的函数关系式为R=
x;
(2)过点C作CH⊥AB于H,设⊙O与边BC相切于点G,连接OG,OA、OB、OC,如图2,
则有OE⊥AB,OF⊥AC,OG⊥BC.
在Rt△AHC中,
HC=AC•sin∠HAC=8×
=4
,
AH=AC•cos∠HAC=8×
=4,
∴BH=AB-AH=10-4=6.
在Rt△BHC中,
BC2=BH2+CH2=36+48=84,
∴BC=2
.
∵S△ABC=S△ABO+S△BCO+S△ACO,
∴
AB•CH=
AB•OE+
BC•OG+
AC•OF,
∴10×4
=10R+2
R+8R,
解得:R=3
-
,
∴当⊙O与△ABC三边相切时,⊙O的半径R为3
-
;
(3)由(2)可知:当⊙O与△ABC三边相切时,R=3
-
.
此时,由R=
x得x=
R=9-
,
∴x的取值范围为0<x≤9-
.

根据切线的性质可得:∠AEO=∠AFO=90°,
根据切线长定理可得:∠EAO=∠FAO=
| 1 |
| 2 |
在Rt△AEO中,
tan∠EAO=
| OE |
| AE |
| R |
| x |
| ||
| 3 |
∴R=
| ||
| 3 |
则⊙O的半径R与EA的长x之间的函数关系式为R=
| ||
| 3 |
(2)过点C作CH⊥AB于H,设⊙O与边BC相切于点G,连接OG,OA、OB、OC,如图2,
则有OE⊥AB,OF⊥AC,OG⊥BC.
在Rt△AHC中,
HC=AC•sin∠HAC=8×
| ||
| 2 |
| 3 |

AH=AC•cos∠HAC=8×
| 1 |
| 2 |
∴BH=AB-AH=10-4=6.
在Rt△BHC中,
BC2=BH2+CH2=36+48=84,
∴BC=2
| 21 |
∵S△ABC=S△ABO+S△BCO+S△ACO,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴10×4
| 3 |
| 21 |
解得:R=3
| 3 |
| 7 |
∴当⊙O与△ABC三边相切时,⊙O的半径R为3
| 3 |
| 7 |
(3)由(2)可知:当⊙O与△ABC三边相切时,R=3
| 3 |
| 7 |
此时,由R=
| ||
| 3 |
| 3 |
| 21 |
∴x的取值范围为0<x≤9-
| 21 |
点评:本题主要考查了切线的性质、切线长定理、三角函数、勾股定理等知识,运用等积变换是解决第(2)小题的关键,考虑临界位置是解决第(3)小题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
在0,-1,-x,
a,3-x,
,
中,是单项式的有( )
| 1 |
| 3 |
| 1-x |
| 2 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,AD=CD,AC平分∠DAB,求证:DC∥AB.
如图,AD=CD,AC平分∠DAB,求证:DC∥AB.