Question

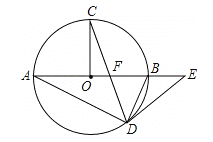
【题目】如图，抛物线与轴交于、两点，与交于点，且，点是轴上的一个动点，当的值最小时，的值是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

作出点C关于x轴的对称点C′，连接C′D交x轴于点M，根据轴对称性及两点之间线段最短可知此时CM+DM最小；

由ED∥y轴得到△C′OM∽△DEM，进而得到=，将各线段的长代入该式进行求解即可.

∵点A（-1，0）在抛物线y=x2+bx-2上，

∴×(-1)2+b×(-1)-2=0.

解得b=-.

∴抛物线的解析式为：y=x2-x-2，

配方得：y= (x-)2-，

∴顶点D的坐标为（，-）.

作出点C关于x轴的对称点C′，则C′（0，2），OC′=2，连接C′D交x轴于点M，

根据轴对称性及两点之间线段最短，可知CM+DM的值最小.

∵ED∥y轴，

∴△C′OM∽△DEM，

∴=.

∵OM=m，EM=-m，OC′=2，ED=，=，

∴=.

解得m=.

故答案选B.