Question

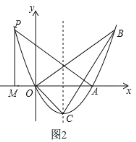
【题目】如图，已知抛物线经过点，及原点，顶点为．

（1）求抛物线的解析式：

（2）试判断的形式，并说明理由：

（3）是抛物线上第二象限内的动点，过点作轴，垂足为，是否存在点使得以点、、为顶点的三角形与相似？若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】 ；是直角三角形点的坐标为或

【解析】

（1）根据抛物线过A（2，0）及原点可设y=a（x-2）x，然后根据抛物线y=a（x-2）x过B（3，3），求出a的值即可；
（2）利用两点间距离公式OB2=18，OC2=2，BC2=20，利用勾股定理逆定理即可得出结论．
（3）分△PMA∽△COB和△PMA∽△BOC表示出PM和AM，从而表示出点P的坐标，代入求得的抛物线的解析式即可求得t的值，从而确定点P的坐标．

根据抛物线过及原点，可设，

又∵抛物线过，

∴，

∴，

∴抛物线的解析式为；由知抛物线解析式为；

∴，

∵，，

∴，，，

∴，

∴是直角三角形．由知，为直角三角形，，且，

①如图，

若，

∴，

∴，

设，则，

∴点，

代入得，

解得（舍）或，

∴的坐标为；

②如图，

若，

∴

设，则，

点，代入得，

解得（舍），，

∴

综上所述，点的坐标为或．