题目内容
2.当x为何值时,代数式$\frac{x-1}{3}$的值与代数式$\frac{3-x}{2}$的值之差不小于2?并用数轴表示.分析 根据题意列不等式$\frac{x-1}{3}$-$\frac{3-x}{2}$≥2,然后解一元一次不等式即可得到x的取值范围,然后用数轴表示解集.
解答 解:根据题意得$\frac{x-1}{3}$-$\frac{3-x}{2}$≥2,
去分母得2(x-1)-3(3-x)≥12,
去括号得2x-2-9+3x≥12,
移项得2x+3x≥12+2+9,
合并得5x≥23,
系数化为1得x≥$\frac{23}{5}$,
用数轴表示为:
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.也考查了用数轴表示不等式解集.

练习册系列答案
相关题目
10.对于任意有理数a,下列结论正确的是( )
| A. | |a|是正数 | B. | -a是负数 | C. | -|a|是负数 | D. | -|a|不一定是负数 |
17.直线l外有两点A、B,若要在l上找一点,使这点与点A、B的距离相等,这样的点能找到( )
| A. | 0个 | B. | 1个 | ||
| C. | 无数个 | D. | 0个或1个或无数个 |
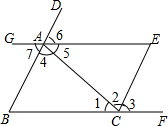 如图,由哪些条件,可得到直线AE∥BF,AB∥CE,直接写出这个条件,不写理由.
如图,由哪些条件,可得到直线AE∥BF,AB∥CE,直接写出这个条件,不写理由.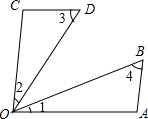 如图,∠1=∠2,CD∥OA,AB∥OC,求证:∠3=∠4.
如图,∠1=∠2,CD∥OA,AB∥OC,求证:∠3=∠4. 已知点A(-1,2),点C(2,1)沿0A方向平移$\sqrt{5}$个单位得出点B,判断四边形0ABC的形状,并证明你的结论;求出直线0A和BC之间的距离.
已知点A(-1,2),点C(2,1)沿0A方向平移$\sqrt{5}$个单位得出点B,判断四边形0ABC的形状,并证明你的结论;求出直线0A和BC之间的距离.