题目内容
有三张正面分别标有数字-1,l,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为未知数的一元二次方程x2-(a2+1)x-a+2的解不为1的概率是 .
考点:概率公式,一元二次方程的解,根的判别式
专题:
分析:首先根据使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为未知数的一元二次方程x2-(a2+1)x-a+2的解不为1确定a的值,然后利用概率公式求解.
解答:解:∵使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,
∴[-2(a-1)]2-4×1×a(a-3)>0,
解得:a>-1,
∵以x为未知数的一元二次方程x2-(a2+1)x-a+2=0的解不为1,
∴12-(a2+1)-a+2≠0,
∴a≠1且a≠-2,
∴满足条件的a只有2,
∴使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为未知数的一元二次方程x2-(a2+1)x-a+2的解不为1的概率是
,
故答案为:
.
∴[-2(a-1)]2-4×1×a(a-3)>0,
解得:a>-1,
∵以x为未知数的一元二次方程x2-(a2+1)x-a+2=0的解不为1,
∴12-(a2+1)-a+2≠0,
∴a≠1且a≠-2,
∴满足条件的a只有2,
∴使关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为未知数的一元二次方程x2-(a2+1)x-a+2的解不为1的概率是
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,∠A=90°,AC=5,BC=13,那么tanB的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若等腰三角形的一边长为3cm,另一边长为6cm,则这个三角形的周长为( )
| A、12cm或15cm |
| B、12cm |
| C、15cm |
| D、18cm |
 如图,已知AC∥BD,∠1=55°,则∠2等于( )
如图,已知AC∥BD,∠1=55°,则∠2等于( )| A、125° | B、115° |
| C、135° | D、145° |
已知Rt△ABC中,∠C=90°,∠CAB=α,AC=7,那么BC为( )
| A、7sinα |
| B、7cosα |
| C、7tanα |
| D、7cotα |
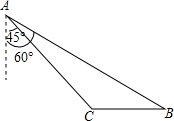 如图所示,2013年4月10日,中国渔民在中国南海huangyandao附近捕鱼作业,中国海监渔船在A第侦察发现,在东南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图所示,2013年4月10日,中国渔民在中国南海huangyandao附近捕鱼作业,中国海监渔船在A第侦察发现,在东南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(