题目内容
18．（1）先化简，再求值：a（1-a）+（a+2）（a-2），其中a=2，．（2）解不等式组：$\left\{\begin{array}{l}{1-2x＞5+3x}\\{3x-2≤6-x}\end{array}\right.$．
分析 （1）原式利用单项式乘以多项式，平方差公式计算得到最简结果，把a的值代入计算即可求出值；
（2）分别求出不等式组中两不等式的解集，找出解集的公共部分即可．
解答 解：（1）原式=a-a2+a2-4=a-4，
当a=2时，原式=2-4=-2；
（2）$\left\{\begin{array}{l}{1-2x＜5+3x①}\\{3x-2≤6-x②}\end{array}\right.$，
由①得：x＜-$\frac{4}{5}$，
由②得：x≤2，
则原不等式的解集为x＜-$\frac{4}{5}$．
点评 此题考查了整式的混合运算-化简求值，以及解一元一次不等式组，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
9．若a与2014的互为倒数，则a的值是（ ）
| A． | -2014 | B． | 2014 | C． | -$\frac{1}{2014}$ | D． | $\frac{1}{2014}$ |
13．
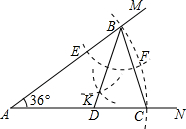如图，小明作图如下：
（1）用量角器作∠MAN=36°；
（2）以A为圆心适当长为半径作圆弧，分别交AM，AN于B，C两点，连结BC；
（3）以B为圆心适当长为半径作圆弧，分别交AB，BC于E，F两点，再分别以E，F为圆心大于$\frac{1}{2}$EF长为半径作圆弧，两条圆弧交于点K，连结BK并延长交AC于点D．
若AD=a，则由以上作图可得AB为（ ）
如图，小明作图如下：（1）用量角器作∠MAN=36°；
（2）以A为圆心适当长为半径作圆弧，分别交AM，AN于B，C两点，连结BC；
（3）以B为圆心适当长为半径作圆弧，分别交AB，BC于E，F两点，再分别以E，F为圆心大于$\frac{1}{2}$EF长为半径作圆弧，两条圆弧交于点K，连结BK并延长交AC于点D．
若AD=a，则由以上作图可得AB为（ ）
| A． | $\frac{\sqrt{5}-1}{2}$a | B． | $\frac{3-\sqrt{5}}{2}$a | C． | $\frac{\sqrt{5}+1}{2}a$ | D． | $\frac{3+\sqrt{5}}{2}$a |
3．一个布袋里放有红色、黄色、黑色三种球，它们除颜色外其余都相同，红球、黄球、黑球的个数之比为5：3：1，则从布袋里任意摸出一个球是黄球的概率是（ ）
| A． | $\frac{5}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{9}$ | D． | $\frac{3}{8}$ |
7．已知点A（-2，y1），B（-1，y2）在函数y=$\frac{3}{x}$的图象上，则y1与y2的大小关系是（ ）
| A． | y1＞y2 | B． | y1＜y2 | C． | y1=y2 | D． | 无法确定 |