题目内容
若实数a，b满足
a-ab+b2+2=0，则a的取值范围是（ ）
| 1 |
| 2 |
| A、a≤-2 |
| B、a≥4 |
| C、a≤-2或a≥4 |
| D、-2≤a≤4 |
考点：根的判别式
专题：
分析：根据题意得到其根的判别式为非负数，据此求得a的取值范围即可．
解答：解：∵b是实数，
∴关于b的一元二次方程b2-ab+
a+2=0，
△=（-a）2-4×1×（
a+2）≥0
解得：a≤-2或a≥4；
∴a的取值范围是a≤-2或a≥4．
故选C．
∴关于b的一元二次方程b2-ab+
| 1 |
| 2 |
△=（-a）2-4×1×（
| 1 |
| 2 |
解得：a≤-2或a≥4；
∴a的取值范围是a≤-2或a≥4．
故选C．
点评：此题考查了根的判别式，掌握一元二次方程根的情况与判别式△的关系：△＞0?方程有两个不相等的实数根；△=0?方程有两个相等的实数根；△＜0?方程没有实数根是本题的关键．
练习册系列答案
相关题目
如图，点A、D、G、M在半圆上，四边形ABOC、DEOF、HMNO均为矩形，设BC=a，EF=b，HN=c，则a、b、c三者间的大小关系为在△ABC中，AD为∠BAC的平分线，DE⊥AB，F为AC上一点，且∠DFA=120°，则DE与DF的关系为（自己画图）（ ）
| A、DE＞DF |
| B、DE＜DF |
| C、DE=DF |
| D、不能确定DE与DF的大小 |
若点A（3-m，n+2）关于原点的对称点B的坐标是（-3，2），则m，n的值为（ ）
| A、m=-6，n=-4 |
| B、m=O，n=-4 |
| C、m=6，n=4 |
| D、m=6，n=-4 |
下列各数中，最小的数是（ ）
| A、1的相反数 | ||
| B、0的相反数 | ||
C、-
| ||
| D、（-3）+4的值 |
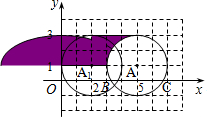如图，在平面直角坐标系中，以A（5，1）为圆心，2个单位长度为半径的⊙A交x轴于点B、C．解答下列问题：