题目内容
1. 如图,在Rt△ABC中,∠B=90°,将AB边沿AD折叠,使点B与点E重合,若AB=8,BC=6,则CD=$\frac{10}{3}$.
如图,在Rt△ABC中,∠B=90°,将AB边沿AD折叠,使点B与点E重合,若AB=8,BC=6,则CD=$\frac{10}{3}$.
分析 先利用勾股定理求得AC=10,然后由翻折的性质得到BD=DE,AE=AB=8,于是得到CE=2,设DC为x,则DE=BD=6-x,最后在三角形DCE中,利用勾股定理列方程求解即可.
解答 解:∵∠B=90°,
∴AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=10.
由翻折的性质可知:BD=DE,AE=AB=8,
∴CE=AC-EA=10-8=2.
设DC为x,则DE=BD=6-x.
在Rt△DCE中,由勾股定理得:DC2=CE2+DE2,即x2=(6-x)2+22,
解得;x=$\frac{10}{3}$.
∴CD=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,在△DCE中,利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
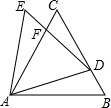 已知:D是等边△ABC中BC边上一个不与B,C重合的动点,且△ADE也是等边三角形.
已知:D是等边△ABC中BC边上一个不与B,C重合的动点,且△ADE也是等边三角形.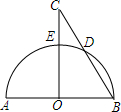 ⊙O直径AB长为6,CO⊥AB,CO=4,求:CD的长.
⊙O直径AB长为6,CO⊥AB,CO=4,求:CD的长.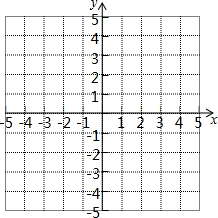 已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、