题目内容
坐标系中有△ABC,A(1,4),B(3,1),C(4,2),有一双曲线y=
与该三角形无交点,则可知k的取值范围是 .
| k |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:先求出各点横纵坐标的积,再求出k的取值范围即可.
解答:解:∵A(1,4),B(3,1),C(4,2),
∴1×4=4,3×1=3,4×2=8,
∵双曲线y=
与该三角形无交点,
∴k<3或k>8.
故答案为:k<3或k>8.
∴1×4=4,3×1=3,4×2=8,
∵双曲线y=
| k |
| x |
∴k<3或k>8.
故答案为:k<3或k>8.
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
化简
,所得的结果为( )
1+
|
A、1+
| ||||
B、1-
| ||||
C、1+
| ||||
D、1-
|
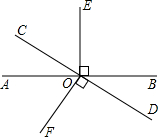 如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD. 如图,两块全等的含30°的三角板ABC和DEF拼接在一起,其中D和B重合,C在DF上,∠ABC=∠FDE=90°,∠A=∠F=30°,BC=
如图,两块全等的含30°的三角板ABC和DEF拼接在一起,其中D和B重合,C在DF上,∠ABC=∠FDE=90°,∠A=∠F=30°,BC=