题目内容
请阅读下面问题的解答过程:已知实数a,b满足a+b﹦8,ab﹦15,且a>b,试求a-b的值.
解:∵a+b﹦8,ab﹦15,∴(a+b)2﹦a2+2ab+b2﹦64.
∵a2+b2﹦34,∴(a-b)2﹦a2-2ab+b2﹦34-2×15﹦4.
∵a>b,∴a-b﹦
| 4 |
请仿照上面的解题过程,解答下面问题:
已知x+
| 1 |
| x |
| 1 |
| x |
分析:本题主要考查完全平方公式的应用,要注意公式间的相互转化,即:(x-
)2=x2+
-2=(x+
)2-4,再由平方根的意义求解.
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
解答:解:∵x+
=5,
∴(x+
)2=x2+2+
=25,
∴x2+
=23,
∴(x-
)2=x2-2+
=23-2=21,
(1)当0<x<1时,x<
,x-
=-
;
(2)当x>1时,x>
,x-
=
.
| 1 |
| x |
∴(x+
| 1 |
| x |
| 1 |
| x2 |
∴x2+
| 1 |
| x2 |
∴(x-
| 1 |
| x |
| 1 |
| x2 |
(1)当0<x<1时,x<
| 1 |
| x |
| 1 |
| x |
| 21 |
(2)当x>1时,x>
| 1 |
| x |
| 1 |
| x |
| 21 |
点评:本题考查了完全平方公式,灵活运用完全平方公式通过开方,求得结果.当题中出现两个数的差或和时,一般要用到它们的平方.

练习册系列答案
相关题目
 ﹦2.
﹦2. =5,且x>0,试求代数式x-
=5,且x>0,试求代数式x-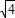 ﹦2.
﹦2.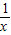 =5,且x>0,试求代数式x-
=5,且x>0,试求代数式x-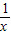 的值.
的值. ﹦2.
﹦2. =5,且x>0,试求代数式x-
=5,且x>0,试求代数式x- 的值.
的值.