题目内容
7. 平行四边形ABCD的对角线AC与BD相交于点O,∠ADB=90°,OA=5,OB=3,求AD和AC的长度.
平行四边形ABCD的对角线AC与BD相交于点O,∠ADB=90°,OA=5,OB=3,求AD和AC的长度.
分析 由平行四边形的性质得出AC=2OA=10,OD=OB=3,再由勾股定理求出AD即可.
解答 解:∵平行四边形ABCD的对角线AC与BD相交于点O,
∴AC=2OA=2×5=10,OD=OB=3,
∵∠ADB=90°,
∴AD2=OA2-OD2.
∴AD=$\sqrt{{5^2}-{3^2}}=4$.
点评 本题考查了平行四边形性质的运用,勾股定理的运用;熟练掌握平行四边形的性质,由勾股定理求出AD是解决问题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.一次函数y=kx-6(k<0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
2.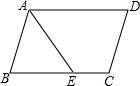 在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )
在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )
 在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )
在平行四边形ABCD中,∠B=80°,AE平分∠BAD,交BC于点E,则∠AEB的度数为( )| A. | 40° | B. | 60° | C. | 50° | D. | 30° |
12.如图标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.某频数分布直方图中,共有A,B,C,D,E五个小组,频数分别为10,15,25,35,10,则直方图中,长方形高的比为( )
| A. | 2,3,5,7,2 | B. | 1,3,4,5,1 | C. | 2,3,5,6,2 | D. | 2,4,5,4,2 |
