Question

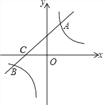
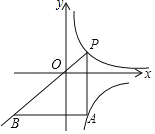
【题目】在平面直角坐标系xOy中，当m，n满足mn＝k（k为常数，且m＞0，n＞0）时，就称点（m，n）为“等积点”．若直线y＝﹣x+b（b＞0）与x轴、y轴分别交于点A和点B，并且该直线上有且只有一个“等积点”，过点A与y轴平行的直线和过点B与x轴平行的直线交于点C，点E是直线AC上的“等积点”，点F是直线BC上的“等积点”，若△OEF的面积为，则OE=______．

Answer 1

【答案】

【解析】

由题意“等积点”在反比例函数的图象上，直线y＝x＋b（b＞0）与x轴、y轴分别交于点A和点B，并且直线有且只有一个“等积点”，可得B（0，），A（，0），E（，），F（，），“等积点”M的坐标为（，），根据△OEF的面积＝S正方形AOBC2S△AOES△EFC＝，列方程求出k即可解决问题．

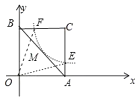
解：如图，由题意，“等积点”在反比例函数的图象上，

∵直线y＝x＋b（b＞0）与x轴、y轴分别交于点A和点B，并且直线上有且只有一个“等积点”，

∴方程即有两个相等的实数根，

∴，即，

∴B（0，），A（，0），E（，），F（，），“等积点”M的坐标为（，），

∵△OEF的面积＝S正方形AOBC2S△AOES△EFC＝，

∴，

解得：k＝2或（舍弃），

∴E（，），

∴OE＝，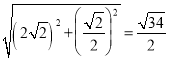

故答案为：．