题目内容
15.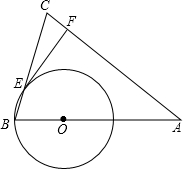 如图,点O在△ABC的边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC于F,直线EF是⊙O的切线.
如图,点O在△ABC的边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC于F,直线EF是⊙O的切线.(1)求证:△ABC为等腰三角形;
(2)若BD=2DA,cosB=$\frac{1}{3}$,CF=2,求线段AF的长.
分析 (1)连结OE,如图,根据切线的性质得OE⊥EF,而EF⊥AC,则可判断OE∥AC,根据平行线的性质得∠OEB=∠C,加上∠B=∠OEB,所以∠B=∠C,于是可判断△ABC为等腰三角形;
(2)先在Rt△CEF中,利用余弦的定义可计算出CE=3CF=6,再根据平行线分线段成比例定理,由OE∥AC得$\frac{BE}{EC}$=$\frac{BO}{OA}$=$\frac{1}{2}$,则BE=$\frac{1}{2}$CE=3,连结DE,如图,由BD为直径得到∠BED=90°,则利用余弦定义可计算出BD,从而得到AB和AC的长,再利用AF=AC-CF进行计算即可.
解答 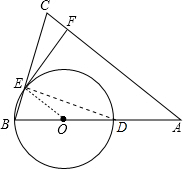 (1)证明:连结OE,如图,
(1)证明:连结OE,如图,
∵直线EF是⊙O的切线,
∴OE⊥EF,
∵EF⊥AC,
∴OE∥AC,
∴∠OEB=∠C,
∵OE=OB,
∴∠B=∠OEB,
∴∠B=∠C,
∴△ABC为等腰三角形;
(2)解:在Rt△CEF中,∵cosC=cosB=$\frac{1}{3}$=$\frac{CF}{CE}$,
∴CE=3CF=6,
∵BD=2DA,
∴BO=OD=AD,
∴OE∥AC,
∴$\frac{BE}{EC}$=$\frac{BO}{OA}$=$\frac{1}{2}$,
∴BE=$\frac{1}{2}$CE=3,
连结DE,如图,
∵BD为直径,
∴∠BED=90°,
∵cos=$\frac{BE}{BD}$=$\frac{1}{3}$,
∴BD=3BE=3×3=9,
∴AB=9×$\frac{3}{2}$=$\frac{27}{2}$,
∴AC=AB=$\frac{27}{2}$,
∴AE=AC-CF=$\frac{27}{2}$-2=$\frac{23}{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了解直角三角形与圆周角定理.

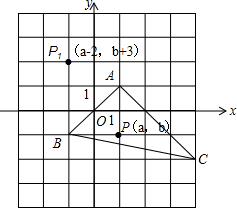 如图所示,△ABC中,任意一点P(a,b)经平移后对应点P1(a-2,b+3),将△ABC作同样的平移得到△A1B1C1.求画出△A1B1C1;并写出A1,B1,C1的坐标;求△A1B1C1面积.
如图所示,△ABC中,任意一点P(a,b)经平移后对应点P1(a-2,b+3),将△ABC作同样的平移得到△A1B1C1.求画出△A1B1C1;并写出A1,B1,C1的坐标;求△A1B1C1面积. | A. | 实际问题→收集数据→表示数据→整理数据→统计分析合理决策 | |
| B. | 实际问题→表示数据→收集数据→整理数据→统计分析合理决策 | |
| C. | 实际问题→收集数据→整理数据→表示数据→统计分析合理决策 | |
| D. | 实际问题→整理数据→收集数据→表示数据→统计分析合理决策 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |


 如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针.若针扎到小正方形(阴影部分)的概率是$\frac{1}{4}$,则大、小两个正方形的边长之比是2:1.
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针.若针扎到小正方形(阴影部分)的概率是$\frac{1}{4}$,则大、小两个正方形的边长之比是2:1.