题目内容
 如图,等腰△ABC中,AB=AC,∠A=34°,线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=34°,线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、39° | B、40° |
| C、45° | D、46° |
考点:等腰三角形的性质,线段垂直平分线的性质
专题:
分析:由条件可先求得∠ABC,再利用线段垂直平分线的性质可知∠ABE=∠A,可求得∠CBE.
解答:解:∵AB=AC,∠A=34°,
∴∠ABC=
=73°,
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=34°,
∴∠CBE=∠ABC-∠ABE=73°-34°=39°,
故选A.
∴∠ABC=
| 180°-34° |
| 2 |
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=34°,
∴∠CBE=∠ABC-∠ABE=73°-34°=39°,
故选A.
点评:本题主要考查等腰三角形的性质及线段垂直平分线的性质,掌握等边对等角是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
无论m取何值,下列各式都有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列一元二次方程中,两实数根的和等于-4的是( )
| A、x2+2x-4=0 |
| B、x2-2x+4=0 |
| C、x2-4x-5=0 |
| D、x2+4x-5=0 |
若x、y为有理数,且|x-2|+(y+2)2=0,则(
)2013的值为( )
| x |
| y |
| A、2013 | B、-2013 |
| C、1 | D、-1 |
近似数98.76万精确到( )
| A、百分位 | B、百位 | C、千位 | D、万位 |
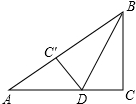 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )