题目内容
如图所示,已知∠A的度数为α,∠AME与∠ANE的角平分线相交于点A1,∠A1ME与∠A1NE的角平分线相交于点A2,∠A2ME与∠A2NE的角平分线相交于点A3,…,依此类推得到点An,则∠A+∠A1+∠A2+∠A3+…+∠An的度数为 .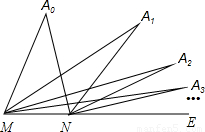
【答案】分析:由∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,而A1B、A1C分别平分∠ABC和∠ACD,得到∠ACD=2∠A1CD,∠ABC=2∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,即∠A=22∠A2,因此找出规律.
解答:解:∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1=α,
∴∠A1= α,
α,
同理可得∠A1=2∠A2,
即∠A=22∠A2=α,
∴∠A2= α,
α,
∴∠A=2n∠An,
∴∠An=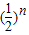 α,
α,
∴∠A+∠A1+∠A2+∠A3+…+∠An=α+ α+
α+ α+
α+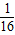 α+…+
α+…+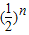 α=
α=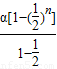 =2α[1-
=2α[1-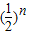 ].
].
故答案是:2α[1-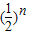 ].
].
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质,难度适中.
解答:解:∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1=α,
∴∠A1=
 α,
α,同理可得∠A1=2∠A2,
即∠A=22∠A2=α,
∴∠A2=
 α,
α,∴∠A=2n∠An,
∴∠An=
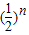 α,
α,∴∠A+∠A1+∠A2+∠A3+…+∠An=α+
 α+
α+ α+
α+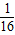 α+…+
α+…+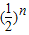 α=
α=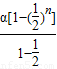 =2α[1-
=2α[1-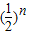 ].
].故答案是:2α[1-
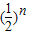 ].
].点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质,难度适中.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
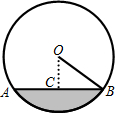 一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )
一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )| A、16 | B、10 | C、8 | D、6 |
 (2012•新化县二模)一条排水管的截面如图所示.已知排水管的截面圆半径OB=100cm,截面圆圆心O到水面的距离OC是60cm,则水面宽AB=
(2012•新化县二模)一条排水管的截面如图所示.已知排水管的截面圆半径OB=100cm,截面圆圆心O到水面的距离OC是60cm,则水面宽AB= (2012•荆州模拟)某工艺品由一个底面朝上的圆锥体上方嵌入一圆球组成,其横截面如图所示,已知圆锥的母线AB、AC和球体相切,且与底座夹角均为75°,圆锥体底面的周长为20πcm,求球体的半径(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,结果精确到0.1)
(2012•荆州模拟)某工艺品由一个底面朝上的圆锥体上方嵌入一圆球组成,其横截面如图所示,已知圆锥的母线AB、AC和球体相切,且与底座夹角均为75°,圆锥体底面的周长为20πcm,求球体的半径(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,结果精确到0.1) 如图所示,已知⊙O的半径为30cm,弦AB=36cm,则cos∠OAB等于( )
如图所示,已知⊙O的半径为30cm,弦AB=36cm,则cos∠OAB等于( ) 如图所示,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA等于
如图所示,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA等于