题目内容
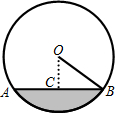
如图所示，已知⊙O的半径为30cm，弦AB=36cm，则cos∠OAB等于（ ）分析：过O作OC垂直于AB，利用垂径定理得到C为AB的中点，求出AC的长，在直角三角形AOC中，利用锐角三角函数定义即可求出所求的值．
解答：
解：过O作OC⊥AB，可得C为AB的中点，
∵AB=36cm，∴AC=
AB=18cm，
在Rt△AOC中，OA=30cm，AC=18cm，
则cos∠OAB=
=
=
．
故选A
解：过O作OC⊥AB，可得C为AB的中点，∵AB=36cm，∴AC=
| 1 |
| 2 |
在Rt△AOC中，OA=30cm，AC=18cm，
则cos∠OAB=
| AC |
| OA |
| 18 |
| 30 |
| 3 |
| 5 |
故选A
点评：此题考查了垂径定理，以及锐角三角函数定义，熟练掌握垂径定理是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一条排水管的截面如图所示．已知排水管的截面圆半径OB=10，截面圆圆心O到水面的距离OC是6，则水面宽AB是（ ）| A、16 | B、10 | C、8 | D、6 |
（2012•新化县二模）一条排水管的截面如图所示．已知排水管的截面圆半径OB=100cm，截面圆圆心O到水面的距离OC是60cm，则水面宽AB=
（2012•荆州模拟）某工艺品由一个底面朝上的圆锥体上方嵌入一圆球组成，其横截面如图所示，已知圆锥的母线AB、AC和球体相切，且与底座夹角均为75°，圆锥体底面的周长为20πcm，求球体的半径（参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，结果精确到0.1）
如图所示，已知⊙O的半径为5cm，弦AB的长为8cm，P是AB延长线上一点，BP=2cm，则tan∠OPA等于